Decomposing the Hadamard gate (advanced)
As we know from our precedent article Introduction to quantum logic gates, conceptually quantum computing operations manipulates Φ and θ of the superposition to move points along the surface of the Bloch unit sphere. In the last article, even if we pointed out the position of the qubit after being applied the Hadamard gate, we did not precise the equivalent operations, in terms of rotations[1].
Say we want to reuse our Pauli-X gate introduced at the beginning of our previous article, then our Hadamard operation could be decomposed as below:
- rotate our up vector |0> of 180 degrees or π radians around the X-axis (Pauli-X gate)
- rotate our vector of -π/2 radians around the Y axis
If we had to rotate the vector of π radians around the Y axis, it would be an easy task: we would only need to apply the Pauli-Y matrice, which by definition, equates to a rotation around the Y-axis of the Bloch sphere by π radians (it maps |0> to i|1> and |1> to -i|0>). So how can we do?
Actually, more generally, the Pauli- X, Y and Z matrices are so-called because when they are exponentiated, they give rise to the rotation operators, which rotate the Bloch vector about the x, y and z axes, by a given angle θ. These rotation operators are defined as per below:
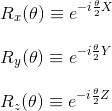
Now, if a operator A satisifies A2 = I, it can be shown that:
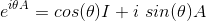
And since all the Pauli matrices satisfy X2 = Y2 = Z2 = I, the rotation operator can be expanded as:
This section of the article is only available for our subscribers. Please click here to subscribe to a subscription plan to view this part of the article.

