In the previous article, we looked at single-qubit quantum gates, like the fundamental Hadamard gate.
We have detailed the way it was applying to one qubit. But let's see how it could operate on two qubits, by example on |00>.
As we know already from our previous article Expectation value of a product state, the final state will be the tensor product of the two transformed single-qubit states.

which can be developed to:
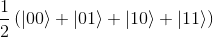
So by applying the Hadamard gate to two qubits, we generate the superposition of all four basis states of the tensor product of the sub-states, with an equiprobability of (1/2)2 = 0.25 of the computational basis states |0> and |1>.
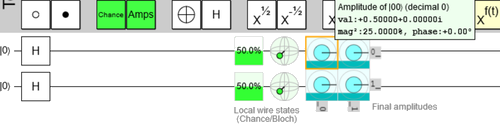
Below is this quantum circuit visualized in the Quirk browser. Quirk confirms that the probability that the result state collapses to one of the four basis vectors equals to 25%.
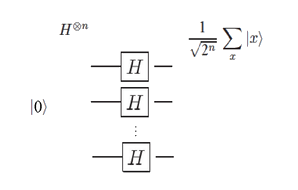
Remark 1: More generally, starting with a state of n qubits |0...0n⟩, if we apply the Hadamard gate to each qubit it results in the following state:

We end up with 2n observable basis states. Many quantum algorithms use the Hadamard transform as an initial step, since it maps n qubits initialized with |0> to a superposition of all 2n orthogonal states in the |0>,|1> basis with equal weight.
See by example the Deutsch-Jozsa algorithm.
Remark 2: When two gates are in parallel, like in the previous case, we can consider the tensor product of the two gates and apply that on the 2-qubit state vector, as per the method exposed in Tensor Product Matrices. We'll end up with the same result[1]
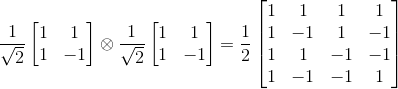
Now applying this matrix to the two qbits states, we get:
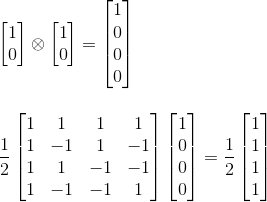
which is strictly equivalent to:
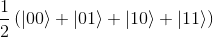
More generally, it can be proved that the general equation for the Hadamard gate transformation on multiple qubits is:
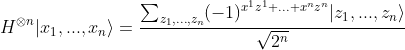
which can be summarized more succinctly in the very useful equation
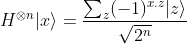
where x.z is the bitwise inner product of x and z.
Let's try to verify this result for a few cases.
If n=1, we know that
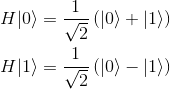
Which can be formulated this way as well
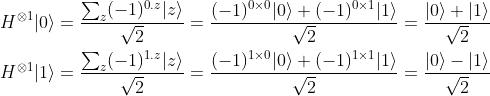
Checking now for n=2, we get:
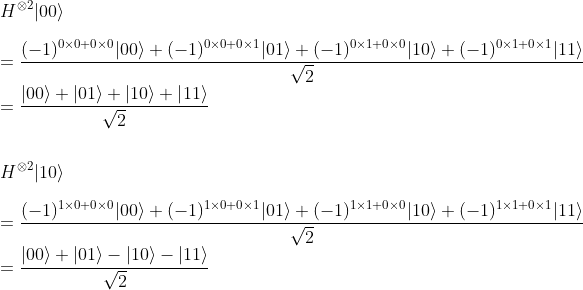
[1] This way of applying the tensor product of the gates is even more general that the first way we exposed by applying each gate on each sub-system, since if the two input qubits are entangled, we won't be able to represent the input state as a tensor product of the states of the two qubits.

