Dans notre précédent article Énergie relativiste (partie 2), nous avions choisi deux quantités E/c=γmc et P=γmv afin de déterminer l'expression générale de l'énergie d'une particule - qu'elle soit dotée de masse ou non.
En note, nous avions également signalé que ces deux quantités n'avaient pas été choisies au hasard mais consituaient les composants de la généralisation en quatre dimensions de la quantité de mouvement newtonienne, le vecteur quadri-moment ou quadri-impulsion.
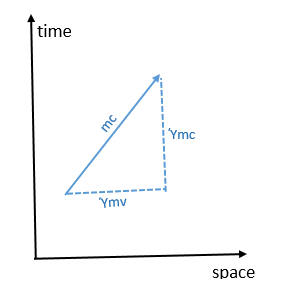
Nous aurions alors la composante temporelle du quadri-vecteur quantité de mouvement égale alors à l'énergie relativiste et les trois autres composantes spatiales représentant la quantité de mouvement relativiste p.
Remarque: A des vitesses suffisamment faibles, on remarque que les composantes spatiales de la quadri-quantité de mouvement se ramènent aux composantes correspondantes de la quantité de mouvement newtonienne:
px = mvx, py =mvy, pz = mvz.
et la quadri-quantité de mouvement représente donc a priori une généralisation relativiste acceptable du concept newtonien de quantité de mouvement.
Il nous reste à interroger plus avant la conservation de la quadri-quantité de mouvement
Conservation de la quadri-impulsion
Nous avons constanté précédemment dans notre article Quantité de mouvement relativiste (partie 2) deux éléments importants:
- tout d'abord que la conservation de la quantité de mouvement newtonienne n'était pas compatible avec le principe de relativité: à cause de la transformation relativiste des vitesses, si la quantité de mouvement newtonienne est conservée dans un référentiel inertiel, alors elle ne l'est pas dans un autre.
- nous avons a contrario montré la conservation des composantes spatiales du vecteur quadri-impulsion - à condition que la masse de la particule finale vérifie M=2γm.
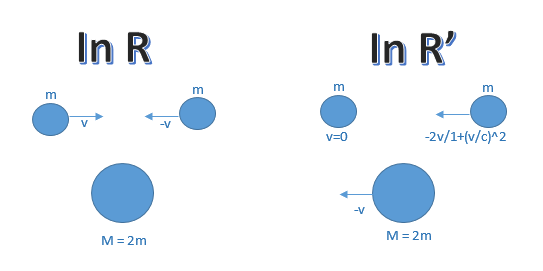
Vérifions à présent que la composante temporelle du quadri-momentum ou autrement dit l'énergie relativiste se conserve bien dans R'. Dans notre cas, cela revient à vérifier la première ligne de l'équation de conservation du quadri-moment générale suivante, en notant u la vitesse de composition relativiste u=2v/(1+(v/c)2)
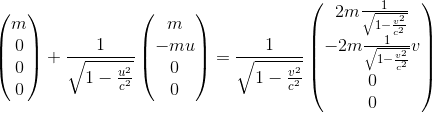
soit donc dans notre cas en isolant la première ligne i.e le composant temps ou énergie du quadri-moment
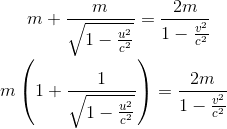
En choisissant c=1 pour faciliter les calculs, on montre facilement avec u=2v/1+v2 que:
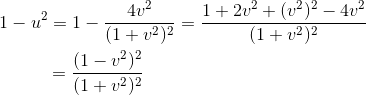
En remplaçant 1-u2 dans l'expression de gauche (énergie des deux particules avant le choc inélastique) on obtient bien:
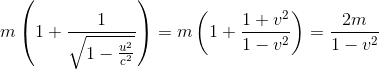
CQFD

