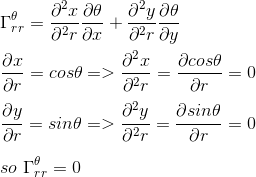Dans cet article, afin de se familiariser avec le concept du Symbole de Christoffel présent dans l'équation des géodésiques, on se propose d'en calculer les différents coefficients dans un cas tout d'abord simple, celui d'un système de coordonnées polaires planes.
D'après la formule du symbole de Christoffel, on sait que l'on doit calculer a priori huit composants, puisque chaque indice β, μ et ν du symbole peut prendre les valeurs r et θ:
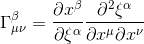
On peut ainsi résumer l'ensemble des coefficients à trouver dans les deux matrices ci-dessous:
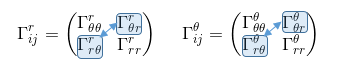
D'après la définition des symboles de Christoffel, ceux-ci sont symétriques sur les indices du bas (les dérivées partielles qu'ils représentent sont commutatives), ce qui laisse au final six coefficients indépendants à trouver.
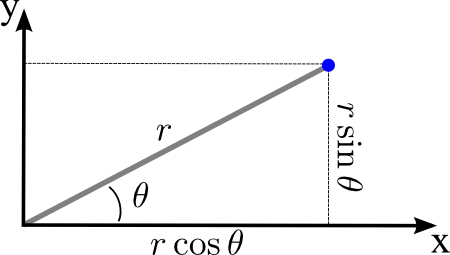
Avec x = r cosθ et y = r sin θ, calculons d'abord les quatre composants de la première matrice, en n'oubliant pas de sommer l'indice muet α sur les coordonnées x et y :

De même:
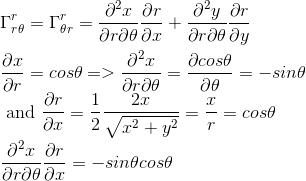
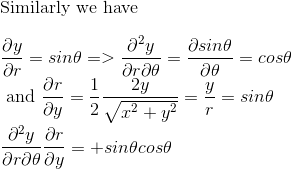
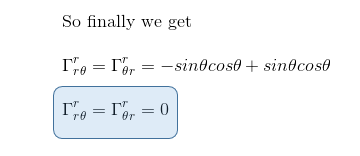

On obtient ainsi la première matrice recherchée avec un seul élément non nul:
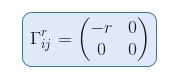
Intéressons-nous maintenant à la seconde matrice
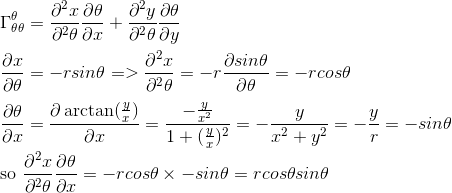

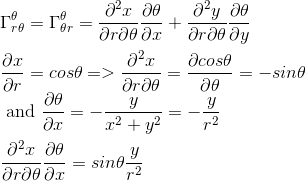
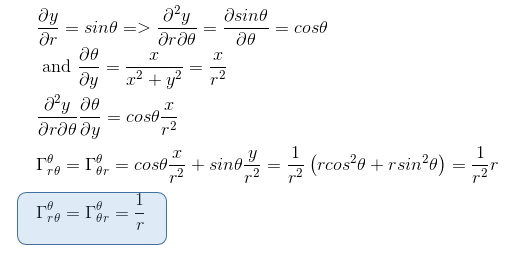
Le calcul du dernier coefficient Γθrr nous donne