Je suis récemment tombé sur ce livre de référence de Kip S. Thorne - co-lauréat du prix Nobel 2017 de physique pour son travail sur les ondes gravitationnelles, Modern classical physics.
Le site de Princeton University Press en a gracieusemnt et gratuitement mis le premier chapitre en ligne, et bien lui en a pris.

Dans ce chapitre, Thorne y expose la physique newtonienne d'un point de vue géométrique. Par cela, if faut comprendre que Thorne se propose d'exprimer toutes les quantités et lois physiques sous une forme géométrique, c'est-à-dire indépendamment d'un quelconque système de coordonnées ou de vecteurs de base.
C'est l'occasion pour Thorne d'énoncer son Principe Géométrique, dont il affirme qu'il constitue le socle de la physique de Newton, et en même temps de son llivre:
|
Principe Géométrique: toutes les lois de la physique constituent des relations géométriques entre objets géométriques (scalaires, vecteurs et tenseurs), exprimables sans l'aide d'aucun système de coordonnées |
Cette formulation purement géométrique des lois de la Nature implique pour ces lois, selon Thorpe, le double avantage:
- d'être exprimées beaucoup plus clairement et élégamment que dans un système de coordonnées donné
- d'être contraintes directement par la logique mathématique sous-jacente (géométrie différentielle)
On reconnaît ici le principe de covariance tel que postulé par Einstein à la base de la théorie de la relativité générale et Thorne admet lui-même qu'il en constitue le pendant newtonien.
Formuler les lois de la physique indépendamment des référentiels entraîne immanquablement, comme on le sait, l'introduction du concept de tenseur.
Après avoir défini un tenseur de rang-n comme une fonction multilinéaire de n-vecteurs à valeur réelle, Thorne en donne une image plus parlante:
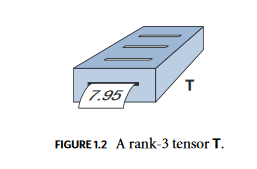
Il faut imaginer un tenseur T de rang n comme une sorte de boîte percée de n fentes sur la face du dessus, au sein desquelles sont insérés n vecteurs, et une seule fente sur la face centrale, qui imprime un nombre réel unique, qui n'est autre que la valeur que le tenseur T a évaluée comme fonction des n vecteurs insérés.
De plus, pour illustrer la linéarité du tenseur, si on considère par exemple un tenseur T de rang-3, sa valeur par rapport aux vecteurs A,B,C est dénotée T(A,B,C) et sa linéarité peut s'exprimer sous la forme suivante:
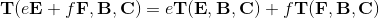
Plutôt simple non?

