Twin paradox part I

In this article, we will expose an apparent paradox related to two twins, but without considering any frame acceleration (this so called 'twin paradox' will be discussed in the next article in part 2).

The apparent paradox is the following:  if two persons are born at the same time in a given 'rest' referential R but with one of the person moving with uniform velocity v, as both referentials R (rest referential) and R' (moving referential attached to the second person) dilate the time one relative to each other, how different will be the twins' ageing process in each referential?

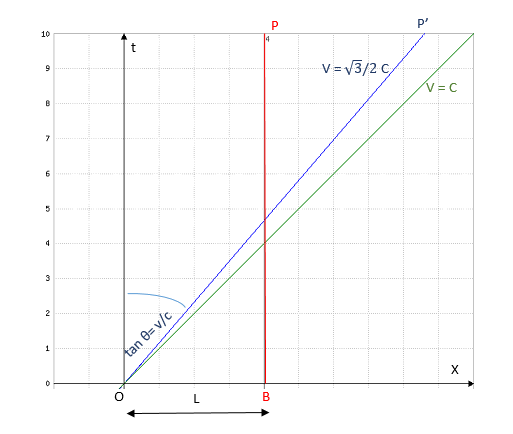
Here we consider two persons born at the same time t=0  in the same referentiel, but one of the person P'  is born in a rocket animated with a uniform movement with velocity v relative to the rest frame (considered to be the Earth), whereas the other one P is born on Earth, say along the x-absciss at the point B with coordinates (0,L), and stay immobile there, watching rockets flying  in the space for the rest of his life.

We take the hypothesis that the relative velocity is given so that Lorentz factor = γ = 2.

SpaceTime diagrams

If we were to draw the spacetime diagrams of these two people P and P', we should then recall from our previous article The Lorentz transformations Part V - 2nd observer in Minkowski spacetime diagram that if an object has a velocity v defined as

But as we know the value of γ = 2, then we deduce immediately that 1-β² = (1/4) => β² = (3/4)  => β = (v/c) = (√3/2).

So the tangent of the wordline of the person born in the rocket to the ct axis equals (√3/2) and the equation of the wordline is ct = (2/√3)x (blue line)

And withour any calculus, we can draw the word line of the second person P staying immobile at the surface of the Earth as a  verticale line with absciss x = L (red line)

The green line, with equation ct = x, is the light wordline.

Time dilation in R

We are now interested into the moment when observer P sees P' in the sky above him.