Previously, we have exposed the The Deutsch-Jozsa algorithm, one of the first example of an algorithm exponentially faster (1 evaluation) than any possible deterministic classical algorithm (2n-1+1 evaluations). It was a great finding, but unfortunately, not of a practical great interest.
In this article, we would like to introduce another quantum algorithm, the so called Grover's algorithm, after the name of its founder, Lov Grover[1].
Compared to the Deutsch alfgorithm, Grover's algorithm belongs to a completely different class of algorithms represented by the quantum search algorithm. These provide a less striking but still remarkable quadratic speedup over the best possible classical algorithms.
Context:
Suppose you are given a large unstructured list of N items. Among these items there is one item with a unique property that we wish to locate; we will call this one the winner w.
To find the winner -- the marked item -- using classical computation, one would have to check on average N/2 of these boxes, and in the worst case, all N of them.
On a quantum computer, however, we can find the marked item in roughly √N steps with Grover's amplitude amplification trick.
Principle:
The 'database' or unstructured list is comprised of all the possible computational basis states our qubits can be in. For example, if our list contains 4 items, the list is the states |00>, |01>, |10>, and |11>. More generally, if the list is composed of 2N items, the list will contain the 2N states of N starting qubits.
The winner state w will be identified by a function f such as:
f(x) = 0 for x != w
f(x) = 1 for x = w
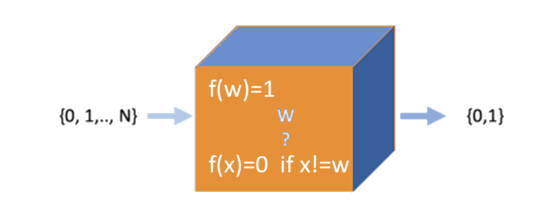
Oracle
In our quantum circuit, this function will be implemented as an Oracle that add a negative phase to the solution state.
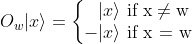
This section of the article is only available for our subscribers. Please click here to subscribe to a subscription plan to view this part of the article.
By definition f(x)=0 or f(x) =1, ff we set the Oracle qubit |y> in the state 1/√2(|0> - |1>)
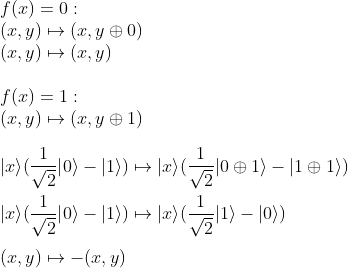
By examining both outputs, we can generalize the equation as:
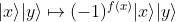
We regard |x⟩ as flipped, thus the oracle qubit |y> is not changed, so by convention the oracle qubits are usually not mentioned in the specification of Grover's algorithm.
Thus the operation of the oracle is simply written as:
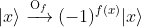
[1] Grover, Lov K. (1997). "A framework for fast quantum mechanical algorithms". https://arxiv.org/abs/quant-ph/9711043. Grover has been ranked as the 9th most prominent computer scientist from India.

