In this article, our goal is to implement the teleportation quantum algorithm as exposed in our last article The quantum teleportation algorithm with the java Strange API already used to implement the entanglement state in this article Java quantum program to entanglement.
You can find all the java technical details and how to run this program at this adress: https://github.com/cyrilondon/quantum-mechanics-java/tree/master/teleportation
As a reminder, that is how our teleportation quantum circuit looks like:
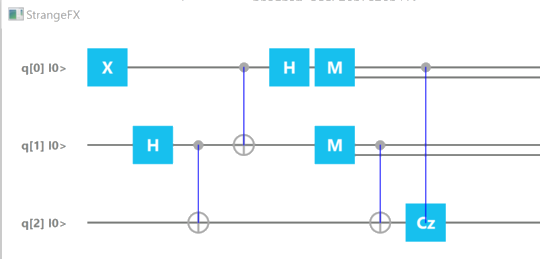
If you have read carefully our previous article, you will notice that we have placed an initial gate P auli-X before the teleportation circuit, so that the qubit to be teleported, at the left of the top ligne is in the |1> state (X|0> = 1).
So once our program run, the expected result should be for Bob (bottom line of the circuit) to get a |1> qubit.
Let's go through our circuit step by step:
First we initialize our quantum simulator (yes we still don't have a personal quantum computer.. ;), and start with 3 qubits all in initial state |0>. Keep in mind that in Strange API each qubit will be indexed respectively at postion 0,1 and 2.
QuantumExecutionEnvironment simulator = new SimpleQuantumExecutionEnvironment();Program program = new Program(3);
Than we switch our first qubit (top line, index=0), the one to be teleported to |1> by applying the Pauli-X gate
Step step0 = new Step();step0.addGate(new X(0));program.addStep(step0);
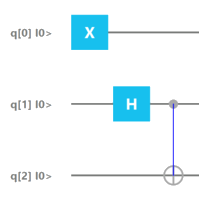
Next we create the entangled pair shared by the second and third qubits. We should know how to do that by know: we apply the H Hadamard gate to the second qubit (index=1) and apply the C-Not gate to the second (index=1) and third gate (index=2)
Step step1 = new Step();step1.addGate(new Hadamard(1));Step step2 = new Step(); step2.addGate(new Cnot(1,2));
So far, we have covered this part of the diagram
Let's go on by applying the last two gates before the measurement.
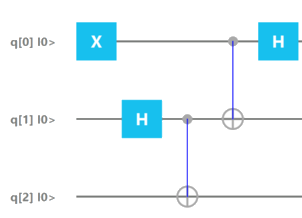
We have to apply the C-Not on the first and second qubits, and then the Hadamard gate on the first qubit.
Step step3 = new Step();step3.addGate(new Cnot(0,1));Step step4 = new Step();step4.addGate(new Hadamard(0));
It's now time to measure the qubit[0] and qubit[1]
Step step5 = new Step();step5.addGate(new Measurement(0));step5.addGate(new Measurement(1));
There are only two gates left to apply, the C-Not gate between the second and third qubit and the Pauli-Z gate between the first and third qubits.

Step step6 = new Step(); step6.addGate(new Cnot(1,2)); step step7 = new Step(); step7.addGate(new Cz(0,2));
We are done with the quantum teleportation algorithm itself. We just have to run the algorithm now and to check that Bob's qubit will be in the |1> state, which in this case maps to the measure of the bit 1.
To make sure that we have enough confidence in our algorithm, we display the statistical results of 1000 simulated executions of our quantum teleportation
Result result = simulator.runProgram(program);Qubit[] qubits = result.getQubits();Qubit q_Alice1 = qubits[0];Qubit q_Alice2 = qubits[1];Qubit q_Bob = qubits[2];int v_Bob = q_Bob.measure();System.out.println("Bob's qubit measured = " + v_Bob );Renderer.showProbabilities(program, 1000);
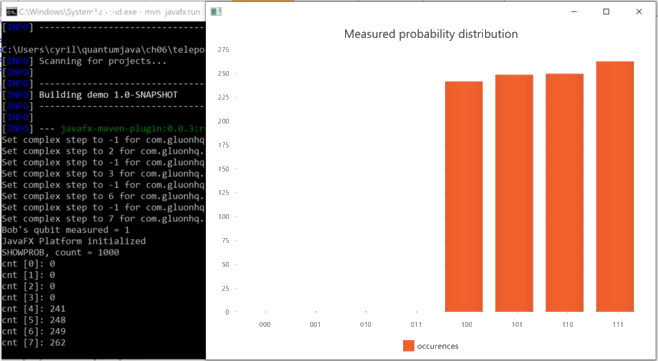
Of those 1000 runs, there are:
- about 250 runs that have the outcome 100, which means qB was measured 1 and both qA and q were measured 0
- about 250 runs with outcome 101, which means qB was measured 1, qA was measured 0 and q were measured 1
- about 250 runs with outcome 110, which means qB was measured 1, qA was measured 1 and q were measured 0
- about 250 runs with outcome 111, which means qB was measured 1, and both qA and q were measured 1.
Note that in all those cases qB is measured 1. The other qubits can hold either 0 or 1, but qB is always 1.
These results seem to confirm that the algorihm we have programmed is indeed teleporting a qubit from Alice to Bob.
Teleportation of a superposition
Actually, we have just showed that the algorithm is working when the initial qubit is in |1> state, but can we do the same if the qubit is on a superposition?
This actually possible with Strange API: instead of applying a gate, you can just initialize the qubit in the α|0> + β|1> superposition state with some specific values for α and β.
For example, adding the following line of code just before our program is run
program.initializeQubit(0, .866);
will initialize out first qubit (index=0) with the value α set to √3/2 = 0.866
Following Max Born's rule, the probability to measure 0 is the square of α, which means in our case 3/4=75% chance to measure 0 and therefore 25% chance to measure 1.
If we run the modified program, we see the following output:
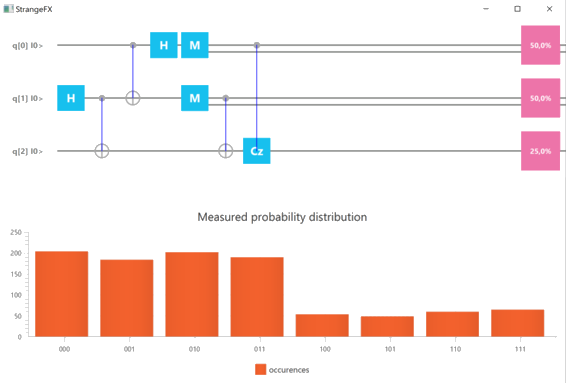
From the top half of the output, we see that there is now a probability of 25% that Bob’s qubit will now be measured as 1.
The bottom part of the figure shows a similar result: Bob's qubit measured as 1 corresponds to the last four combinations 100,101,110 and 111 and sum up roughly to 250.
This is exactly what we hoped for!

