As our ultimate goal is to formulate a relation between the spacetime geometry and its content, we first have to find the right mathematical tool to describe this spacetime content.
In Special Relativity, we have seen in our article Introduction to Four-momentum vector and E = mc2 that mass, energy and momentum are all related, as expressed in the energy momentum relation:
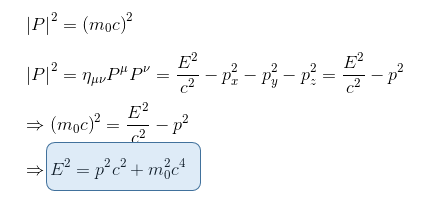
It therefore seems reasonable to make the hypothesis that the source of the gravitational field in General Relativity should include momentum and energy as well as mass.
On the other hand, the equivalent Newtonian equation describing the gravitational potential caused by a mass density ρ, as expressed by Poisson's equation is:
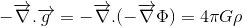
So the following question arises: is the equivalent relativistic energy density to be found also a scalar quantity or a tensor component?
To answer this question, let us consider a volume dx x dy x dz of non-interacting particles at rest with respect to each other, commonly referred to as "dust cloud".
In its own referential S, this cloud has an energy density ρ0=m0n0 where m0 refers to the mass of a dust particle and n0 the number of particles by unit of volum. By definition, as the cloud stands at rest in its proper referential, there is no kinetic term.
In a different Lorentzian referential S' moving with constant velocity v in the x-direction, Lorentz transformation will lead to:
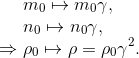
The first γ factor relates to the Lorentzian energy transformation, as seen in Introduction to Four-momentum vector and E = mc2
The second γ factor is caused by the length contaction in the x direction, which makes the new dust volum observed from S' equals to dx/γ x dy x dz and therefore multiply the new density by the same factor.
Obviously, ρ is not a scalar in which case it would be invariant. It can not be neither a four-vector component, in which case he would transform linearly with γ factor. Actually ρ behaves like a component of a rank-2 tensor (rank-2 tensors transform like a product of two Lorentz transformations). More pecisely, in this case, ρ behaves like a tt- componentof a rank-2 tensor.
Writing the four-velocity vector uμ of the dust cloud in the S' referential, we get:
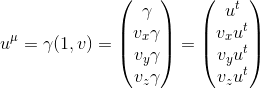
so we can set γ = ut
Using this equality and that the energy of each particle equals pt = mut, we can rewrite the total energy density in S':
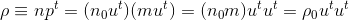
We therefore are able confirm that this quantity could be interpreted as the tt-component of a symetric rank-2 tensor:
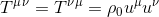
This is the energy-momentum tensor, also known as the stress-energy tensor for the dust.
Physical meaning of the energy-momentum tensor
Because the stress–energy tensor is of order two, its components can be displayed in 4 × 4 matrix form:
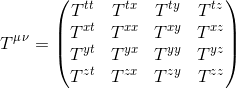
As seen previsouly, Ttt represents the density of relativistic mass, i.e the energy density. But what can represent all the other 15 components of the energy momentum tensor?
Let us consider the Ttx component first; we can write:
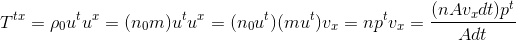
The quantity Avxdt represents the dust volum which goes across the surface A perpendicular to the x-direction during the dt time interval, so that Avxdt represents the total number of particles which goes through this surface.We can then interpret Ttx = Txt as the total energy per unit of surface and of time, i.e. the flux of energy per unit area per unit time in the x-direction. A similar argument applies to Tty and Ttz, respectively the flux of energy across per unit area per unit time of y and z = constant.
For the other components, let’s consider Tkl where k and l are spatial indices. In this case, we have
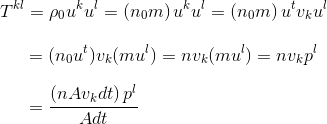
The first factor is the flux per unit area per unit time of particles in the k direction, so Tkl is the flux in the k direction of l momentum. For example, Txz is the flux of z momentum in the x direction (or, since T is symmetric, the flux of x momentum in the z direction).
Covariant divergence of the energy-momentum tensor
In flat spacetime of special relativity, the fundamental laws of conservation of energy and momentum (i.e. there are flows but no sources or sinks of energy-momentum) could be epxressed by saying:
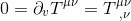
That's a consequence of Noether's theorem concerning the invariance of physical systems with respect to spatial translation (in other words, that the laws of physics do not vary with locations in space), which gives the law of conservation of linear momentum.
Using the 'comma goes to semi-colon' rule, we get the following tensor equation, which by the Principle of General Covariance will hold true for any coordinate system, therefore will stay valid in curved spacetime of general relativity.
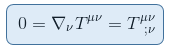
Remark: Although the energy-momentum tensor has a zero divergence in curved spacetime does NOT imply a true conservation law as it does in special relativity. This is because in curved spacetime there is the gravitational energy, that is NOT included in the energy-momentum tensor.

