Geodesics in Schwarzschild spacetime

               We saw in our previous articles Geodesic equation and Christoffel symbols and Geodesic that geodesic equations describe the paths of free falling particles in spacetime.

In order to understand how objects move in Schwarzschild spacetime, we therefore require the geodesic equations defined by the Schwarzschild metric.

We have shown that those equations are in the form of parameterised curves ^[1]

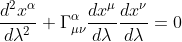
Replacing α by the four variables t, r, φ and θ gives us four complicated-looking differential Schwarzschild equations

For α = t, looking at the values of Γ^t_μν from our previous article, we see that only Γ^t_tr and Γ^t_rt are not null, leading to

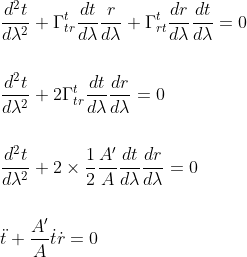
Looking at α = r, we know that the four diagonal elements of the matrix Γ^r_μν are not null

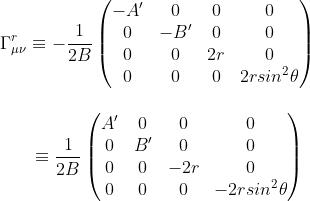
 so that we can write

 If we replace now α by θ, and reminding us the Γ^θ_μν matrix, we can write

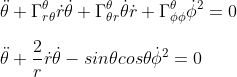
Finally, we retrieve the last geodesic equation by replacing α by Φ

Newtonian approximation in case of radial free fall

Radial free fall implies the object is moving 'straight down', ie Φ is constant, therefore dΦ/dλ = 0 and so h = r²(dΦ/dλ) = 0

And the last equation thus reduces to

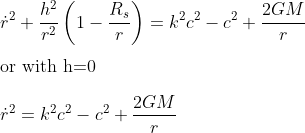
We can differentiate this equation with respect to τ, giving

which should remind you something very familiar in Newtonian mechanics ;-)

[1] To be more precise, time-like geodesics (where ds² > 0 and proper time dτ ≠ 0)  describe the paths of massive objects  and can use proper time as a affine parameter. Null geodesics (where ds² = 0 and proper time dτ = 0) describe the paths of (massless) photons and need another parameter. In the rest of the article, we use λ for either.