Nous avons déjà présenté la dilatation des durées dans notre article Introduction à la dilatation des durées et au facteur de Lorentz
Dans cet article, nous nous proposons de revenir sur ce phénomène de dilatation du temps mais à l'aide cette fois-ci d'un diagramme d'espace-temps, un peu comme nous l'avions fait pour présenter la fin de la simultanéité dans La fin de la simultanéité par les diagrammes d'espace-temps.
On se rappelle tout d'abord d'après l'article Quadri-vecteur et intervalle d'espace-temps que l'équation d'intervalle d'esapace-temps est de la forme suivante 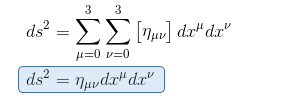
soit encore en développant 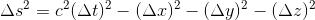
En se limitant aux dimensions temps et abscisse (ct et x), on reconnaît immédiatement l'équation de deux hyperboles de la forme:
c2t2 - x2 = b2 (intervalle de genre temps avec ds2 > 0)
c2t2 - x2 = -a2 (intervalle de genre espace avec ds2 < 0)

Chaque hyperbole relie ainsi tous les événements qui ont un intervalle d'espace-temps égal par rapport à un événement situé l'origine. Les deux hyperboles passant par les points x=a et x=-a relient tous les points d'intervalle espace-temps égal à -a2 et les deux hyperboles passant par les points x=b et x=-b relient entre eux tous les points d'intervalle espace-temps b2.
Considérons à présent le schéma ci-dessous représentant un référentiel S' (axes ct' et x') en mouvement rectiligne uniforme par rapport au référentiel S (axes ct et x).
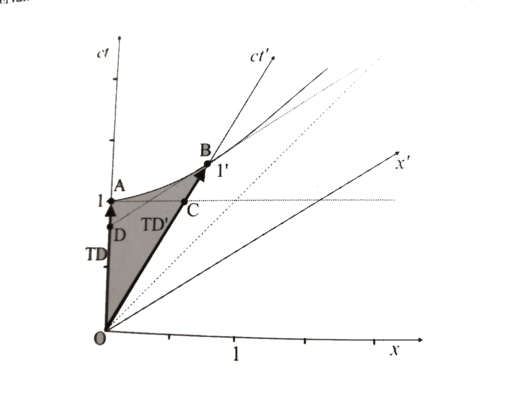
Si l' on suppose que le point A se situe à l'ordonnée ct=1 (x=0) alors b2, l'intervalle d'espace-temps du point A à l'origine doit être lui-même égal à 1 (on rappelle que ds2 = c2t2 - x2). Et parce que l'hyperbole relie entre eux tous les points de même intervalle espace-temps, alors le point B situé sur l'axe ct' (x'=0) doit nécessairement avoir lieu à ct'=1 (ds'2 = 1 = c2t'2 - x'2 = c2t'2 )
D'autre part la ligne en pointillés AC représente la ligne de simultanéité pour l'observateur O, c'est-à-dire que tous les événements qui y figurent ont tous la même valeur temporelle ct=1 alors que la ligne en pointillés BD (tangente à la parabole et parrallèle à l'axe Ox') représente quant à elle la ligne de simultanéité pour l'observateur 0', avec tous les événements y figurant qui ont pour valeur ct'=1.
Ceci étant posé, qu'observe alors chaque observateur dans son propre référentiel?
- L'observateur O' du référentiel S' mesure l'événement C se produisant à un instant ct'<1 (puisque OB=1') sur son axe cr'. Pourtant, l'observateur 0 mesure ce même événement se produisant à l'instant ct=1. Du point de vue de l'observateur O, les horloges dans le référentiel S' sont ralenties.
- Inversement, l'observateur O du référentiel S mesure l'événement D se produisant à un instant ct<1 (puisque OD=1). Pourtant, l'observateur O' mesure ce même événement se produisant à l'instant ct'=1 (point B). Du point de vue de l'observateur O', les horloges dans le référentiel S indiquent un temps dilaté.
CQFD.

