En fait, le vecteur Quadri-impulsion que nous venons de voir dans l'article précédent n'est qu'un cas particulier d'un objet appelé quadrivecteur, omniprésent dans le langage mathématique de la relativité restreinte.
Ce dernier possède deux propriétés:
1) il intègre la coordonnée temporelle aux trois coordonnées spatiales du vecteur élémentaire à trois dimensions qui relie deux points dans l'espace.
Par convention, le temps est la première composante de la liste et on notera le quadri-vecteur avec un indice grec, qui signifie que l'indice peut prendre l'une des quatre valeurs 0, 1, 2 ou 3:
On écrira donc par exemple Xμ = (X0, X1, X2, X3) les composantes du quadrivecteur position Xp, qui sont aussi les coordonnées contravariantes[1] (ct, x, y, z) du point P dans une base inertielle.
2) il est invariant sous les transformations de Lorentz, c'est-à-dire qu'un quadrivecteur est un ensemble quelconque de composantes Aμ qui se transforment ainsi lors d'une transformation de Lorentz le long de l'axe x:
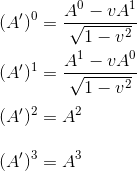
En définissant la matrice Λμν la matrice 4x4 suivante

nous pouvons écrire la transformation de Lorentz suivant l'axe x qui transforme le quadrivecteur A en A' de la manière concise suivante:
(A')μ = [Λμν] Aν[2]
pourvu que notre matrice de transformation soit définie de la façon suivante:

Intervalle d'espace-temps
En définissant Ψv la rapidité associée à v telle que tanh Ψv = v/c, on peut écrire γ = cosh Ψv et γβ = sinh Ψv de sorte que la matrice de boost le long de l'axe x peut se réécrire sous la forme suivante:
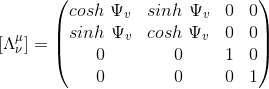
ce qui met en exergue l'analogie avec une rotation: les transformations de Lorentz en configuration standard se comportent ainsi comme des "rotations hyperboliques".
Cette réécriture et l'identité cosh2α - sinh2α permettent de conclure que les coordonnées (t, x, y, z) et (t', x', y', z') d'un même évènement dans deux référentiels inertiels en configuration standard sont telles que:
c2t2 - x2 - y2 - z2 = c2t'2 - x'2 - y'2 - z'2
Et puisque les transformations de Lorentz sont linéaires, il existe une égalité semblable si l'on considère deux événements A et B distincts, de coordonées séparées par (Δt, Δx, Δy, Δz) dans un référentiel inertiel R et par (Δt', Δx', Δy', Δz') dans un autre référentiel inertiel R'. On peut donc écrire cette égalité fondamentale
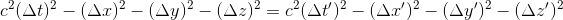
Etant donnés deux événements et leurs coordonnées dans un même référentiel inertiel, on définit par conséquent l'intervalle spatio-temporel Δs2 qui les sépare par:
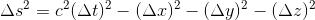
Il s'agit d'une grandeur scalaire dont la valeur ne dépend pas du référentiel dans lequel on le détermine. On dit que c'est un invariant pour les transformations de Lorentz.
Métrique de Minkowski
En relativité restreinte, l'intervalle de longueur ds2 et son invariance sous les transformations de Lorentz permettent de définir une notion de pseudo-norme pour les quadrivecteurs. En effet, à l'aide des coordonnées contravariantes et de la notation indicielle, l'expression de ds2 se remet sous la forme:
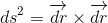
que l'on peut encore développer en
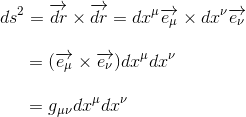
Dans le cas particulier de la relativité restreinte, on gμν qui se note ημν et qui vaut donc d'après l'expression de l'invervalle d'espace-temps:

On peut donc écrire l'intervalle d'espace-temps en relativité restreinte sous la forme:
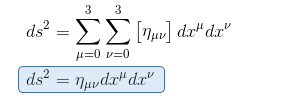
[1] On verra dans un article ultérieur que la modification, opposée à celle des vecteurs de base, que subissent les coordonnées lors d'une transformation de Lorentz explique qu'on les nomme contravariantes.
[2] On vérifie qu'une telle équation est bien formée. Le membre de gauche possède un indice libre μ, pouvant prendre les valeurs 0, 1, 2 ou 3. Le membre de droite possède quant à lui deux indices μ et ν. L'indice de sommation ν n'est pas une variable explicite dans l'équation, mais représente l'indice muet de la convention de sommation d'Einstein. En d'autres termes, chaque côté de l'équation possède un indice contravariant libre, μ et par conséquent cette équation est bien formée.

