We have mentioned that relativistic effects have been observed so far only into the realm of subatomic particles because those are the only ones that physicians are able to accelerate to very high speed in their laboratories.
But in theory, nothing prevents these effects of special relatiivity to apply equally well to things the size of humans. And even more, as Brian Cox states it in his book E=mc2, we could rely on these strange effects for our own survival!

As we now know it, the Sun is roughly middle aged and will remain fairly stable for more than another five billion years. However, after hydrogen fusion in its core has stopped, the Sun will undergo severe changes and become a red giant. It is calculated that the Sun will become sufficiently large to engulf the current orbits of Mercury, Venus, and possibly Earth. It means that if humans have not become extinct by some other reasons by then, it will become a necessity for us to escape our beloved home and to journey to some other stars. But which stars?
If we did not know anything about special relativity, we would say that there would be a very little chance to be able to travel to any of the 200 billion stars that the Milky Way contains. For the very simple reason that our galaxy has a diameter usually considered to be about 100,000–120,000 light-years, and that we could barely be expected to travel to the edges of the galaxy that would take light itself 100,000 years to reach.
But imagine that one day we could build a spaceship that could send us into space at speeds very close to the speed of light (and we have 4 billions years to figure out how), then the theory of special relativity tells us that distance to the stars would shrink, all the more so when we get close to the speed of light.
In this context, it becomes even conceivable to reach the neighboring Andromeda Galaxy, almost 2.5 million light-years away.

as seen by NASA's Wide-field Infrared Survey Explorer
As an exercise, let's try to figure out how fast we would need to travel if we don't want to age more than 1 year on the journey to Andromeda.
If we assume that our spaceship is moving with constant velocity relative to the Earth frame (ct,x,y,z), then special relativity applies and we want our Proper time to be equal 1 year, so:
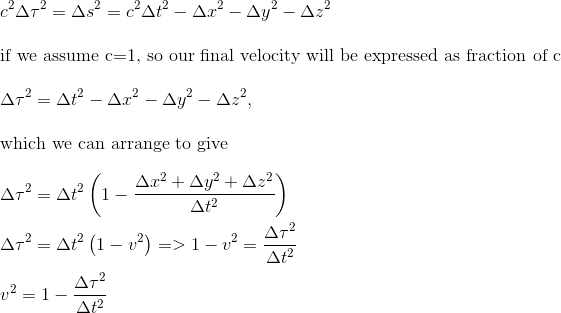
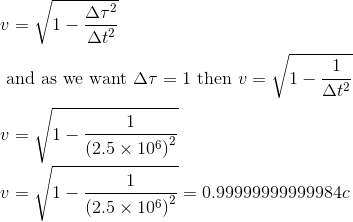
Provided we get a very fast spaceship, Einstein's theory of relativity and subsequent distance contraction makes the travel to distant parts of the Universe imaginable in a way that it never was before!
We end up with this very paradoxal result that by travelling at 0.99999999999984c, so a little bit less than at speed of light, it takes us only 1 year to reach a Galaxy 2.5 million light years away, whereas by definition it takes light itself 2.5 milion years to travel the same distance.

