The equation giving the distance between two points in a particular space is called the metric. Once we know the metric of a space, we know almost everything about the geometry of the space, which is why the metric is of fundamental importance.
We have already met the function that defines the distance between two points in Minkowski spacetime (see Minkowski's Four-Dimensional Space-Time article): it's the spacetime interval given by the formula
ds2 = c2Δt2 - Δx2 - Δy2 - Δz2
This can be written as ds2 = 1xc2Δt2 - 1xΔx2 - 1xΔy2 -1xΔz2
And +1, -1, -1, -1 can be defined as the diagonal elements of a 4x4 matrix, denoted by ημν:
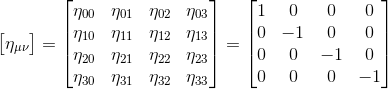
The indices μ,ν after the η symbol identify the elements of the matrix by reference to its rows (μ) and its columns (ν). The convention is that the metric coefficients run from 0 to 3, so η00=1, η11=-1, η22=-1, η21=0, etc.
This matrix simply tells us how to multiply the differentials cdt, dx, dy, dz to obtain the spacetime interval equation. We can see it by writing the matrix product as follow:

So finally, as only η00, η11, η22 and η33 are not null, we get the product equals to
1xc2Δt2 - 1xΔx2 - 1xΔy2 -1xΔz2 = c2Δt2 - Δx2 - Δy2 -Δz2
which is the spacetime interval defining Minkoswki spacetime.
Finally, using the index notation, the Einstein convention (implicit summation on repetead indices) and the Minkowski metric ημν , we can write the Minkowski line element in a more compact form:
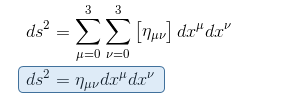
Recall that the symbol ημν irefers specifically to the Minkowski metric.

