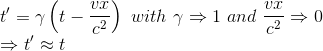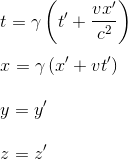Note: the presentation of the Lorentz transformation is done by Einstein in chapter 11 of his book Relativity
Remember that since the beginning, we are trying to find the relationships between the coordinates of an event in two inertial frames R and R', with R' moving with a velocity v with respect to R.
After having spent time giving some insight into the strange nature of the spacetime and of his contruitive effects, it is now time to give a more precise algebraic formulation of how coordinates change for different inertial observers.
This set of equations are called the Lorentz transformations, named after the Dutch physicist Hendrik Lorentz (Nobel Prize 1902)
Given the assumptions that R and R' are in standard configuration, i.e:
- - An observer in frame of reference R defines events with coordinates t, x, y, z
- - Another frame R' moves with velocity v relative to R, with an observer in this moving frame R' defining events using coordinates t', x', y', z'
- - The coordinate axes in each frame of reference are parallel
- - The relative motion is along the coincident xx' axes
- - At time t = t' =0, the origins of both coordinate systems are the same
If an observer in R records an event t, x, y, z , then an observer in R' records the same event with coordinates t', x', y', z' defined as below:
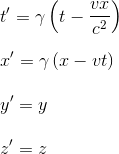 |
With y = Lorentz factor having been already defined in the previous article Constant Speed of light - Introduction to Time Dilation and Lorentz factor

According to principle of relativity, there is no privileged frame of reference, so that the transformations from R to R' must take exactly the same form as the transformation from R' to R.
The only difference is R' moves with velocity -v relative to R (same magnitude but is oppositely directed). So that if an observer in R' records an event in t', x', y',z' then an observer in R records the same event with coordinates
|
|
The reciprocal transformations from each referential relative to the other coud be visualised in a synthetic manner as follow:
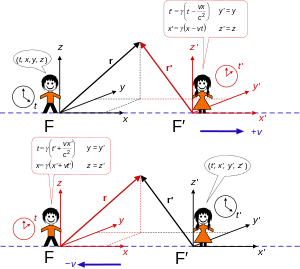
Remark 1: Compared to the classical Galilean physics with absolute time, we begin to understand what Minkowski meant by the union of the two concepts.
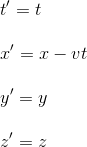
Remark 2: When v<<c, i.e when the relativistic effects fade away, we can verify that the Galilean transformation can be derived from the Lorentz transormations.