In our previous article EPR Paradox, we exposed the counterintuitive predictions of quantum mechanics about strongly correlated systems as they were first discussed by Albert Einstein in 1935, in a joint paper with Boris Podolsky and Nathan Rosen.
However, the three scientists did not coin the word entanglement, nor did they generalize the special properties of the state they considered. Following the EPR paper, Schröndinger wrote a letter [1] to Einstein in German in which he used the word Verschränkung (translated later by himself as entanglement) to describe
the correlations between two particles that interact and then separate, as in the EPR experiment.
In this article, we would like to expose gently[2] the basis of the theory which underlies this very special correlation.
Even if the EPR paradox invokes the formal language like System I and System II, we will prefer instead lighter-weight, informal language like Alice and Bob.
We assume that Alice's system is described by a space of states called SA, and similarly Bob's system is described by a state-space called SB.
Although Einstein's EPR paper was about describing two particles with the observables position and momentum, let's suppose for simplicity that Alice's system consists of a quantum coin of a finite[3] two-dimensional space of states defined by the two basis vectors H (for head) and T (for tail). As it is a quantum mechanical coin, it can exist in superposition and we can thus write its state as:

We can choose Bob's system to be a coin as well, but let's assume it is something different, like a six-sided dice. Bob's Hilbert space of states SB would then be six-dimensional, with each state being decomposed on the folllowing basis:
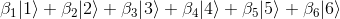
Now if we were to consider these two systems to exist no more independently, but as a composite system, how could we construct the state-space SAB for this combined system?
We have to form the tensor product of the two state-spaces SA and SB, and we note this operation:

This tensor product has a dimension of (SA dimension x SB dimension), so in our example 2 x 6 = 12, and with the following orthonormal basis, built up from the tensor product of the basis vectors from each sub-space:
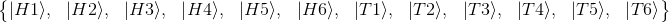
From a more general point of view, for two Hilbert spaces of states HA and HB with the respective basis {|i>A} and {|j>B}, the most general state of the composed system HA x HB is of the form:

That's it. We know enough to lay down our first fondamental rule about entanglement

To make it more clear, let's go back to our example of Alice and Bob
Product state
The following state
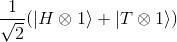
is definitely NOT an entangled state as it can be easily factorized as the product of the two following states, belonging respectively to SA and SB

Entangled state
Can we say the same thing of this state:

Assuming it could be written as a product state, we should find the complex numbers αH, αT, β1and β2 such as:

It is easy so we can not find those numbers, as we get some immediate contradictions:
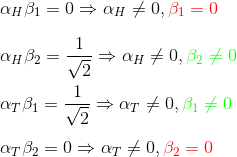
As the state - call it S2 -

can not be written as a product state of two states from SA and SB, we are certain that S2 is a entangled state.
And here comes all the strangeness of the entanglement: if Alice decides to observe the system in her own {H,T} basis, there are two possible outcomes, occuring with equal 1/2 probability (1/√22)
- Alice measures the eigenvalue corresponding to |H> - say 1, and the all system collapses to the combined state |H2>
- Alice measures the eigenvalue corresponding to |T> - say 0, and the all system collapses to the combined state |T1>
If the former occurs, then any subsequent measurement by Bob, in his own basis, will always return 2 (assuming the eigenvalue of |2> is 2).
If the latter occurs (Alice measures 0, the eigenvalue associated to the the eigenvector |T>), then Bob's measurement will return 1 with certainty (assuming the eigenvalue of |1> is 1).
Although the outcome of Alice's measurement is random, the outcome of the entire system is not. That's what puzzled Einstein so much in his EPR article.
Conclusion: The principles of quantum mechanics allow us to superpose basis vectors in more general ways than just product states.
All those states which can not be factorized as a product of two (or more) states are said to be entangled.
Another way of saying that is an entangled state is a complete description of the combined system - no more can be known about it -, where nothing is known about the individual subsystems.
[1] Letter from Erwin Schrödinger to Albert Einstein, 7 june 1935
[2] Gently means without too much mathematical abstraction, but it is however assumed that the reader should have some familiarity with some basic concepts as state vector, Dirac bra-ket notation, observables and Pauli matrices.
[3]Position and momentum observables have both infinte number of eigenvalues and this could make their mathematical notation a little bit more complex - as in the EPR paper. This complexity is however not necessary to understand the basis of the entanglemant phenomenon, which could be perfectly explained in the context of finite dimensionnal Hilbert spaces.

