For any point m in a spacetime Riemannian manifold M, there exists a local coordinate system at m such that:
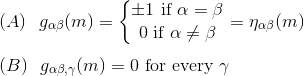
we call such a coordinate system a local inertial frame or a normal frame.
Remark1: the possibility of the existence of this local referential is fully demonstrated in our article Local Flatness or Local Inertial Frames and SpaceTime curvature.
Remark2: as all the first order derivatives of the metric are null, given the Christoffel symbol expression:
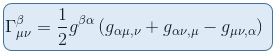
then in a local inertial referential the vanishing of the partial derivatives of the metric tensor at any point of M is equivalent to the vanishing of Christoffel symbols at that point and in this referential the geodesics are straight lines.
Remark3: if the metric first derivatives can always been nullified, it is not the case for all the second derivatives which can only be nullified in a flat spacetime (refer to the same above article for more details)
Remark4: below is a link to an excellent youtube tutorial which gives an overview of how a local inertial frame (black colour) can be obtained by a general coordinate transformation at any point P of a spacetime manifold (blue colour)

