In General Relativity, these are the curves that a free particle (that is, a particle upon which no force acts, where ‘force’ in this case excludes gravity, since the effects of gravity are felt entirely through the curvature of space-time) will follow in a curved space-time .
A geodesic could be equivalently defined as:
- a line which generalizes the notion of a "straight line" to curved spacetime. From this perspective, we have been through the way to derive the geodesic equation directly from the Equivalence Principle in Geodesic equation and Christoffel symbols.
- a time-like wordline that maximizes the Proper Time (EigenZeit) between two given events[1]. See our article Geodesic equation from the principle of least action for the full derivation.
- a line that parallel transports its tangent vector along itself. See Geodesics from covariant derivative for the full derivation.
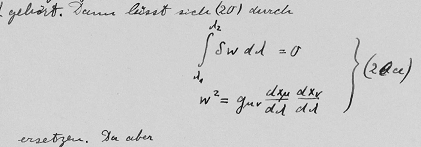
[1] Refer to our article Geodesics as proper time maximization to see how this applies also in Special Relativity.

