| In which it is shown that electricity and magnetism can no more be separated than space and time. |
The aim of this article is to express the relativistic version of the classical Lorentz force law, which says that the force F on a test particule of charge q and velocity v is given by
F = q(E + v x B)
where E and B denote the ordinary 3-dimensional electric and magnetic fields (with magnitude E and B, respectively)
Invariant Lagragian
We should start with the simplest possible Lagragian, describing a free particle in the presence of a four-vector field Aμ(t,x).
We know already that the Lagragian of a free particle of mass m can be written as
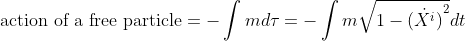
choosing units where c = 1 and (X.i)2 stands for x.2 + y.2 + z.2
On the other hand, when coupling the particle to an electromagnetic field, it looks natural to consider a small part of the particule trajectory, the quadri-vector dXμ, and to combine it with the electromagnetic four-vector Aμ(t,x) = (V/c, -A) - where V is the scalar potential and A the magnetic vector potential - to bring up a scalar, infinitesimal quanity dXμAμ(t,x) - which as per special relativity principle, should remain invariant per Lorentz transformation.
Multiplying this action by the q electric charge yields to

If we bring together the two distinct parts, we get the whole action as
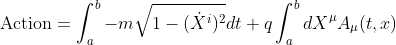
Dividing the second integral by dt yields to

As we know that the action is defined as the integral of the Lagrangian L for an input evolution between the two times a and b, we can easily identify the Lagrangian for our particule as:
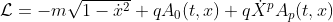
The easiest thing to do now is guess what, resolve the Euler-Lagrange equation!
This section of the article is only available for our subscribers. Please click here to subscribe to a subscription plan to view this part of the article.

