So far we have seen how free particles move in spacetime, and it led us to the concept of geodesic. But we have to understand in more details how these two concepts are related.
We recall that the geodesic equation for a particule with mass is
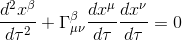
As we know that in General Relativity gravity is equivalent to spacetime curvature , can we then affirm that if all the Christoffel symbols are null, then spacetime is flat, as we have verified in our article Geodesic exercise part I: calculation for 2-dimensional Euclidean space for a two-dimensional Euclidean space - in which geodesics are straight lines?
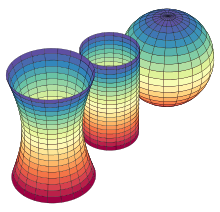
- Source wikipedia
2-surface Gaussian curvature
In fact, what we are looking for is the generalization for the four-dimensional spacetime of the two-dimensional Gaussian curvature, e.g a way of determining the intrinsic measure of curvature, depending only on distances that are measured on the surface, not on the way it is embedded in any space.
If you take a flat piece of paper and bend it gently, it bends in only one direction at a time. At any point on the paper, you can find at least one direction through which there is a straight line on the surface. You can bend it into a cylinder, or into a cone, but you can never bend it without crumpling or distorting to the get a portion of the surface of a sphere.
In Gaussian terms, the cyclinder curvature - defined as the product K1K2 of the two principal curvatures - is null because one of these principals - the one along the axis of the cylinder - is null.
In this article, we want to find a test similar to the piece of paper bending used in two dimensions.
In four-dimensional spacetime, the test will be to try to transform a general metric gμν to the Minkowski form ημν by an appropriate coordinate transformation xμ -> x'μ
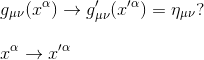
From our previous article Generalisation of the metric tensor in pseudo-Riemannian manifold, we know that the metric gμν has 10 independant components (16 - 6 as the tensor is symmetric.
Also concerning the coordinate transformation xα --> x'α , we have the choice to find a function which relates x'α to (x0, x1,x2 and x3) for each value 0,1,2 and 3 of α.
So we have 4 degrees of freedom to fill 10 conditions, which is generally not possible: as expected, it is generally impossible to reduce a metric describing a curved spacetime to the one of a flat spacetime by a coordinate transformation.
Local Flatness or Local Inertial Frame (LIF)
It appears that we have to be less ambitious and try to find a primed coordinate system that locally only , i.e around a event P in spacetime
- - could reduce the metric g'μν in P to the Minkowski flat spacetime metric ημν
- - and for which all the first derivatives of the metric g'μν are zero
If we take the analogy of the curved surface of the earth, we have to isolate lots of little square patches, each patch being pretty near flat.

We recall from our article Generalisation of the metric tensor in pseudo-Riemannian manifold that an arbitrary metric could be expressed as:

and more generally that the components of a metric tensor in primed coordinate system could be expressed in non primed coordinates as:
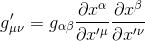
Each of the partial derivatives is a function of the primed coordinates so, for a region close to the event point P, we can expand these derivatives in Taylor series:
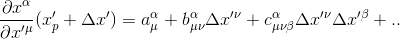
where
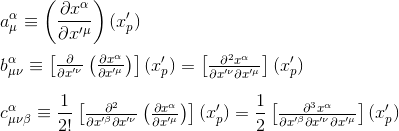
These three quantities represent constant coefficients that we are allowed to choose freely in order to find a local inertial frame around the event P.
Let's try to count the degrees of freedrom we have at each step of this Taylor series development.
This section of the article is only available for our subscribers. Please click here to subscribe to a subscription plan to view this part of the article.