The saga of Einstein's search for his general theory of relativity could have successfully ended as early as in 1913, with the completion of the Outline of a Generalized Theory of Relativity and of a Theory of Gravitation[1], known also as the "Entwurf".
Indeed, in this paper Einstein opens the Section 5 in a very promising way by writing the field equations in the following general form:
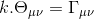
where k is a constant, Θμν is the contravariant stress-energy tensor and Γμν is the still to be found gravitational tensor "which has to be derived from the fundamental tensor gμν by differential operations. In line with the Newton-Poisson law one would be inclined to require that these equations be second-order."
But then Einstein drops his bombshell: "It must be stressed that, it proves impossible to find a differential expression Γμν that is a generalization of ΔΦ and that proves to be a tensor with respect to arbitrary transformations". This assertion being justified by a reference to a particular subsection of Grossman's "Mathematical part" of the paper.
In this passage - see below extract, Grossman notes that the second-rank contraction of Riemann tensor, known as the "Ricci tensor" would be a good candidate to fit the right side of the above field equations, but then rejects this hypothesis as it does not reduce properly into the Newtonian limit.
By this decision, Einstein and Grossman did not know it yet but they had just lost two more years : Einstein would eventually go back exactly to the same point on his 4 November, 1915 paper, by proposing as the gravitationnal tensor, guess what....the Ricci tensor!

[1] Entwurf einer verallgemeinerten Relativitätstheorie und eine Theorie der Gravitation. I. Physikalischer Teil von A. Einstein II. Mathematischer Teil von M. Grossmann's rejection of Ricci tensor as gravitationnal tensor candidate

