As all the information about the spacetime structure is being contained in the metric, it should be possible to express the Christoffel symbols in terms of this metric.
The following calculation is a little bit long and requires special attention (although it is not particularly difficult).
So far, we have defined both the metric tensor and the Christoffel symbols as respectively:
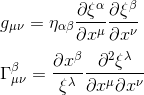
Let's begin by rewriting our metric tensor in the slightly different form gαμ:
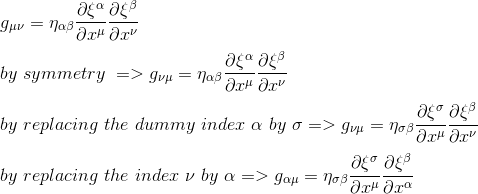
Now, in this second step, we want to calculate the partial derivative of gαμ by xν:
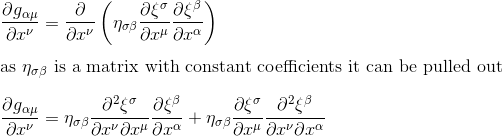
This section of the article is only available for our subscribers. Please click here to subscribe to a subscription plan to view this part of the article.

