As we have done with the end of simultaneity, we want to explore the consequences of assuming that speed of light is constant for all observers, no matter how they are moving relative to each other.
Here we are going to consider what is called a light clock, that is a clock consisting of two mirrors, between which a beam of light bounces back and forth: each bounce of the beam light will be counted as one tick of the clock.

Stationnary referential
From a stationary perspective, the light will travel vertically, up and down.
Say for example that the mirrors are 1m apart, then it will take light 6.67 nanoseconds to complete one round trip i.e. 6.67 * 0.000000001 second.
This is easyly calculated by dividing two times the distance between the mirrors L = 1m by the speed of the light = 299,792,458 meters every second.
This makes actually a very high precision clock, with around 150 millions ticks corresponding to one heartbeat.
Moving referential
Now, imagine putting the light clock on a train travelling very fast along past someone standing on a station platform, at the speed v relative to the ground.
To the stationary observer, the mirrors will appear to be moving and so the light will have to travel further in one tick as shown in the below diagram.
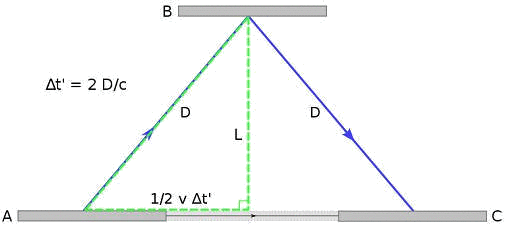
This time, the light will have to travel distance 2*D (and no more 2*L) during one tick.
In order for the clock to tick at the same rate as it does when it is stationnary, the light must travel a little bit faster, but that what is exactly not allowed in Einstein's worldview: the light cannot speed up because the light must be the same for everyone!
So light will still travel the distance D at c speed, and the new time interval Δt' for the light to complete one round trip will be given by:
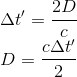
Using Pythagora's theorem for the green triangle, the base being half the distance traveled by the train at the speed v during interval Δt', i.e vΔt'/2:
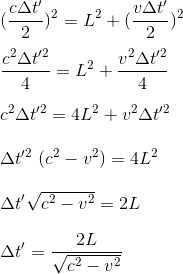
Or we recall that the time taken for one tick of the clock as determined by someone on its own rest referential [1] is simply given by:
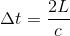
Taking the ratio of these two time intervals tells us by how much the clock on the train is running slow, as measured by someone on the platform

If β is the ratio of v to the speed of light c 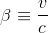
this time dilation equation could be rewritten in the following very common form
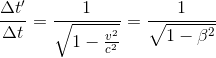
This is a very important quantity in relativity theory, known as the Lorentz factor and is usually represented by the greek letter γ.
 |
Observe that because all objects - except light itself - will travel at less than the speed of light - meaning v is less than c, this γ factor will be larger than 1.
And for most ordinary situations, when v is very small compared to speed of light, γ will stay very close to 1. For example, if the train is moving at 300 kilometres per hour, then we get γ = 1/(1-0.000000000000077)1/2 = 1.000000000000039
Remark: we will find the time dilation effect by another more general way in a further article The Lorentz transformations Part III - Measuring-Rods and Clocks in motion
[1] The time measured by an observer in its own rest frame is called the Proper Time and is noted τ (tau); we will come across this concept in further articles.