A geodesic of spacetime is a curve that is straight and uniformly parametrized, as measured in each local Lorentz frame along its way.
If the geosidesic is timelike, then it is a possible wordline for a freely falling particle, and its uniformly ticking parameter λ (called affine parameter) is a multiple of the particule's proper time, λ = κτ + μ.
This definition of geodesic translates into the abstract and coordinate-free language: a geodesic is a curve P(λ) that parallel-transports its tangent vector u = dP/dλ along itself.
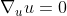
Now defining a coordinate system {xα(P)), along with basis vectors eα = ∂/ ∂xα, we can define the tangent vector u and its components
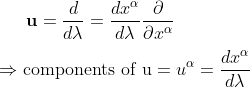
and thus finally the component version of the abstract geodesic equation definition becomes

CQFD
This geodesic equation can be solved (in principle) when both initial data xα and dxα / dλ have been specified.