Dans cet article, nous nous proposons d'introduire aux notions de coordonnées contravariantes et covariantes d'un quadri-vecteur.
Dans l'article précédent, nous avons introduit la notation contravariante d'un quadri-vecteur (avec indice supérieur) ainsi que la métrique de Minkowski ημν (la lettre grecque êta) et qui vaut:

Nous avons vu que cette matrice très simple nous permettait d'exprimer le scalaire intervalle d'espace-temps ds2 sous une forme synthétique à l'aide de la convention de sommation d'Einstein:
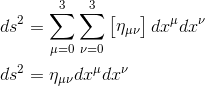
Considérons cette matrice ημν et multiplions-la à présent par le quadrivecteur Av, où ν va de 0 à 3. En utilisant la convention de sommation, nous pouvons écrire
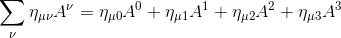
C'est un nouveau type d'objet que nous allons noter Aμ , avec l'indice inférieur :
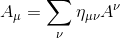
Ce nouvel objet n'est pas l'objet de départ Aν, ce qui serait le cas si la métrique de Minkowski était la matrice identité. Les nombres -1 dans sa diagonale ont pour conséquence que lorsqu'on calcule ce produit, les trois composantes spatiales changent de signe, tandis que la composante temps reste inchangée.
Nous voyons immédiatement que
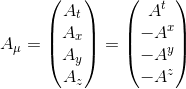
En d'autres termes, lorsque nous effectuons cette opération, nous changeons simplement le signe des composantes spatiales, et nous obtenons alors les composantes dites covariantes du quadri-vecteur.
Remarque 1: nous pouvons écrire l'intervalle d'espace-temps tel que défini précedemment par une formulation encore plus synthétique, puisque ημνdxμ peut tout simplement s'écrire d'après ce qui précéde par dxν et on peut donc écrire:
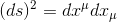
Remarque 2: le procédé qui consiste à passer du quadrivecteur Aμ au scalaire AμAμ est appelé contraction d'indice (on perd une unité d'indice) et il est très général.