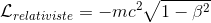Sûrement avez-vous déjà entendu parler du principe de moindre action. Toutes les lois de la physique, de celles de la dynamque de Newton aux théories modernes de jauge des interactions fondamentales se fondent en effet sur ce principe.
Celui-ci stipule que si un système part d'un point a et aboutit à un point b, il va alors "choisir" un chemin particulier parmi tous les chemins possibles. Plus particulièrement, il va choisir le chemin qui minimise la quantité appelée action. Celle-ci se construit par incréments comme une somme sur une trajectoire donnée où l'on considère des chemins infinitésimaux et on calcule l'action en sommant toutes les petites actions attachées à chaque petit chemin ainsi considéré.
Action non relativiste
L'action se définit donc comme une intégrale sur une trajectoire. Reste à déterminer l'intégrande, c'est-à-dire la fonction à intégrer qui dans ce cas est appelée lagrangien et notée L
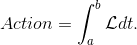
La règle est que le lagrangien ne dépend que de la position et de la vitesse de la particule. Dans le cas le plus simple d'une particule en mouvement libre (non soumis à aucune force), le lagrangien correspond simplement à l'énergie cinétique. On peut donc écrire:
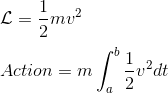
Action relativiste
En relativité restreinte, comme la trajectoire dans l'espace-temps ne dépend pas du référentiel par rapport auquel on l'observe, l'action qui la détermine doit être invariante par changement de référentiel.
Mais il y a qu'une seule chose qui soit invariante lorsqu'une particule passe d'une position à une autre: l'intervalle d'espace-temps les séparant. Ceci suggère une expression de la forme:
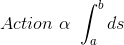
avec la variation infinitésimale de l'espace intervalle-temps s'écrivant:
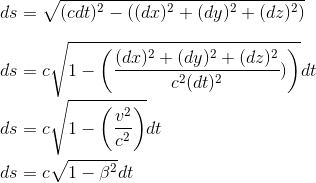
Dans le cas des vitesses faibles où v<<c, on doit retrouver l'action relativistique ci-dessus donc:
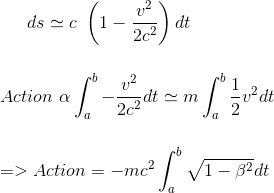
Et l'on en déduit finalement le lagrangien relativiste: