Dans de nombreux cas, il est primordial de savoir comment un vecteur change lorsque l'on se déplace d'une position à une autre. Pour des vecteurs exprimés à l'aide de coordonnées cartésiennes, il est relativement aisé de calculer la dérivée d'un vecteur: on considère simplement la dérivée de chacune de ses composantes. On peut faire cela car les vecteurs de base du système de coordonnées sont partout constants à la fois en magnitude et en direction, et donc l'on n'a pas besoin de se soucier des dérivées des vecteurs de base eux-mêmes.
Mais si l'on se place dans un système de coordonnées polaires par exemple en 2D, les vecteurs de base r et θ pointent dans des directions différentes lorsque l'on se déplace dans le plan, ce qui veut dire que lorsque l'on calcule la dérivée d'un vecteur exprimé dans ces coordonnées, on doit également considérer les dérivées des vecteurs de base.
Consdérons un vecteur A quelconque exprimé selon le système de coordonnées x1, x2, x3 à l'aide des vecteurs de base e1, e2 et e3
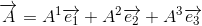
Si l'on considère la dérivée de A par rapport à la coordonée x1, on obtient:
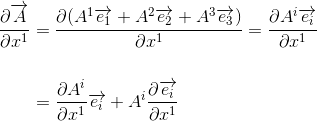
C'est donc le second terme de cette équation qui complique le processus de calculer une dérivée lorsque l'on se trouve dans un système de coordonnées au sein duquel l'amplitude et/ou la direction des vecteurs de bases change lorsque l'on se déplace dans l'espace.
Pour bien comprendre les symboles de Christoffel, il est important de réaliser que la dérivée d'un vecteur de base reste un vecteur. Et donc que comme tout vecteur, celui-ci pourra s'exprimer comme une combinaison des vecteurs de base au point considéré.
Chaque symbole de Christoffel, écrit sous la forme d'un gamma majuscule grec (Γ) n'exprimera alors rien d'autre que le coefficient pondéré d'un de ces vecteurs de base. On aura plus précisément
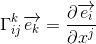
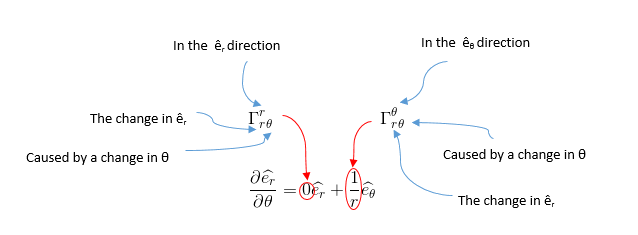
Par exemple, en coordonnées polaires planes on peut écrire:
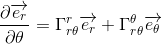
Dans le premier signe Γ, le r en haut indique que ce composant constitue la composante selon le vecteur de base er, le r en bas signifie que l'on dérive le vecteur de base er et le θ en bas indique que l'on dérive selon la composante θ.
Dans le second signe Γ, le θ en haut indique que ce composant constitue la composante selon le vecteur de base eθ, le r en bas signifie que l'on dérive le vecteur de base er et le θ en bas indique que l'on dérive selon la composante θ.