Quantum Teleportation, probably because its name, is the new buzz word in the world of quantum science nowadays. We get breakthrough news almost every week on this topic.
In August 2019, Austrian and Chinese scientists announced that they have succeeded in teleporting three-dimensional quantum states (qutrits) for the first time[1].
Six months later, in Nature Physics, researchers reported the demonstration of chip-to-chip quantum teleportation and multi-photon entanglement on silicon-photonic circuitry.
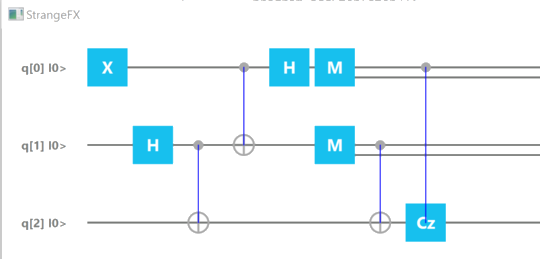
But what do we mean exactly by teleportation? Our aim in this article is to give a gentle introduction to the teleportation topic, and more precisley at the end of this reading, you should be able to understand and implement the teleportation quantum circuit:
Don't worry about its apparent complexity, we have encountered each and every component of this circuit in our previous articles!
The problem setup:
The problem that quantum teleportation looks to solve is as follows: Alice has an unknown qubit |ψ⟩ that she wants to send to Bob. How can she do this?
It’s interesting to note that this is non-trivial in quantum information science, whereas in classical information theory there is no problem at all.
Rather, in a classical world:
- the low-level network drivers of the operating system read the value of the byte at the value specific memory location,
- and they send a serialized copy of that value over a network to the other computer (where it is copied again)
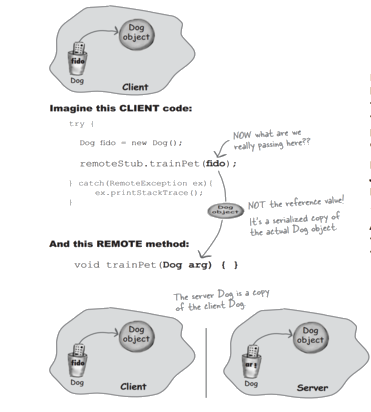
Unfortunately, we can NOT do this with a qubit.
- first because when we make a measurement, we disturb the state of the system according to the fundamental measurement postulate of quantum mechanics: the entire superposition of states collapses to a single term[2]. Hence, by doing so, not only we destroy the original qubit, but we also don’t have enough information to create a new qubit. with the same value.
- and qubits can not easily be transfered over long distances[3].
The No-cloning theorem
Why don’t we just make a copy of it, without measuring it? Well, unfortunately this is what the no-cloning theorem forbids, as easily demonstrated in our article The No-cloning theorem.
The quantum teleportation
Fortunately, there is still a way for Alice to send her unknown qubit to Bob via the interesting result of quantum teleportation.
We assume that the first qubit (the top qubit in the diagram and q[0] in the below diagram) belongs to Alice and starts out in any |ψ⟩ state, since this is what the quantum teleportation algorithm assumes.
The second qubit (q[1] in the below diagram) belongs to Alice as well.
The first thing to do is to share an entangled state between Alice and Bob by doing a Hadamard on the Alice's one and then performing a controlled not gate on Bob"s qubit.

To see that this circuit indeed creates an EPR pair, note that we start out with both qubits in the |00> state.
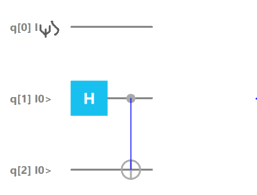
We then have to perform a Hadamard gate on the first qubit and do nothing on the second qubit. Thus, theoverall multi-qubit gate that we perform is H ⊗ I, as we saw previously in this article.
In the lines below A and B stand for Alice and Bob, as the first qubit belongs to Alice (q[1] in the diagram above) and the second qubit belongs to Bob (q[2] in the diagram above).
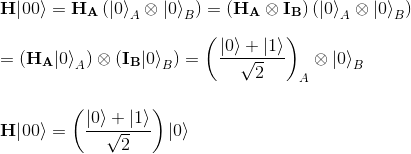
This is almost an EPR pair. To make it exactly an EPR pair, as we know we have to perform a CNOT, controlling on the first qubit. Doing so yields
This section of the article is only available for our subscribers. Please click here to subscribe to a subscription plan to view this part of the article.
To get a better idea of the possible outcomes Alice can get when she will measure, we can group terms containing the same state for the first two terms.
There are four possibilities for the first two qubits, namely |00>,|01>,|10>, and|11>. Grouping these terms together, we can rewrite the state
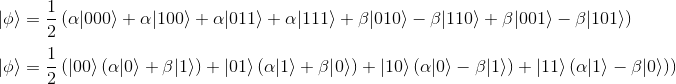
Now Alice measures her two qubits (the first two qubits).
- Suppose she gets the |00> outcome. Then, Bob’s qubit is in the state α|0> +β|1>, which is |ψ> exactly. In this case, we are done, and Alice’s unknown qubit |ψ> has been teleported to Bob.
- Suppose instead Alice measures |01>. By looking at the above expression, we see that Bob’s qubit in this case would be α|1>+β|0>. This is almost |ψ>, but the amplitudes are flipped. How can we get|ψ> exactly from this state? We can perform a NOT gate X(α|1> +β|0>) = α|0> +β|1> =|ψ>.
- If Alice measures |10⟩, Bob’s qubit is in the state α|0⟩−β|1⟩. Further, he can obtain |ψ⟩ by performing a Pauli-Z gate on his qubit. As we have seen in the previous article Introduction to quantum logic gates that will have for effect to negate the |1> basis state to -|1>. That is, Z(α|0⟩−β|1⟩) =α|0⟩+β|1⟩ = |ψ⟩.
- And finally in the case of Alice measuring |11>, Bob would have to apply both the NOT gate and the Pauli-Z gates.That is ZX(α|1⟩−β|0>) =α|0⟩+β|1⟩ = |ψ⟩.
Thus, in all four measurement cases, Bob is able to obtain exactly Alice’s unknown qubit |ψ> without either knowing what the actual state is.
For summarize, we enumerate all measurement possibilities in the table below.
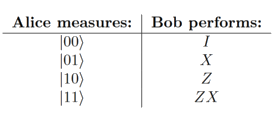
Note that the controlled-gates after the measurements on Alice’s qubits perform exactly these operations.
After the measurement, we have classical information, which we represent in circuit diagrams with two lines (instead of one line for qubits).
The controlled-X and controlled-Z are thus conditional on these measurement outcomes.
If the second qubit comes out to be a zero, then we do NOT perform an X gate on Bob’s qubit. If the second qubit does come out to be one, then we do perform an X gate.
Similarly for the controlled-Z but with the first qubit.
That's it! We have teleported our first qubit ;-)
What can we learn from quantum teleportation? Later on, we will show that quantum computation and quantum information have revealed a plethora of methods for interchanging resources, many built upon quantum teleportation. In particular, we will see how teleportation can be used to build quantum gates which are resistant to the effects of noise, and we will show that teleportation is intimately connected with the properties of quantum error-correcting codes.
Important final remark: Note that there must be some form of classical communication between Alice and Bob after Alice makes measurements and before Bob performs operations.
If Alice measures 00, she has to tell Bob “I measured 00” at which point Bob knows to do nothing. Similarly for the other three possibilities.
Without this communication, Bob would have no idea what to do.
In this sense, it is important to emphasize that no information, classical or quantum, is really being “teleported” here, despite the name of the algorithm.
Alice’s classical “communication” is of course limited by the speed of light, and Einstein's special relativity (which postulates that nothing can go faster than light), is not violated!
[1] Complex quantum teleportation achieved for the first time: https://phys.org/news/2019-08-complex-quantum-teleportation.html
[2] More formally, performing an observation irreversibly collapses the system into some eigenstate of an observable, corrupting the information contained in the qubit(s).
[3]The longer a photon travels over an optical fiber cable, the more likely errors will occur. At present, the maximum distance that can be covered is in the range of 100 km

