In this article, we will write a our first quantum program to bring two qubits in entanglement state.
You can find all the java technical details and how to run this program at this adress: https://github.com/cyrilondon/quantum-mechanics-java
We know from our previous article C-NOT gate, Bell State and Entanglement that in this purpose we have to prepare a two-qubit system by example in |11> state, and then
- apply the Hadamard gate to the first one so we get a 50/50 superposition state
- then apply the C-NOT gate with the second qubit |1> acting as the control qubit
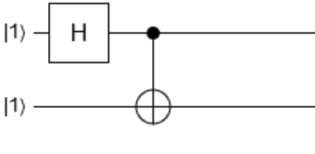
We obtain then the |β11> entangled Bell state.
Java Strange API
For this purpose, we will use the Strange java API, a Quantum Computing API for Java[1] which can be found here https://github.com/gluonhq/strange.
To get an first insight of the library, we can look at the code example given as introduction to the API in the Readme section.
That's a very good example in our case, because it implements the first step to build the entangled Bell state |β11> as exposed in our previous article C-NOT gate, Bell State and Entanglement
This sample create a Program that requires 2 qubits. It will create 2 steps (step1 and step2). The first step adds a Paul-X (NOT) Gate to the first qubit (the first qubit flips from |0> to |1>). The second steps adds a Hadamard Gate to the first qubit (H|1>), and a NOT gate to the second qubit (so we get finally that two-qubit state H|11>. Both steps are added to the Program.
In order to "run" this program, we need a QuantumExecutionEnvironment. Strange comes with a SimpleQuantumExecutionEnvironment which contains a very simple, non-optimized quantum computer simulator.
private static void runH11() { Program p = new Program(2); |00> Step step1 = new Step(); step1.addGate(new X(0)); X|00>=|10> p.addStep(step1); Step step2 = new Step(); step2.addGate(new Hadamard(0)); H|10> step2.addGate(new X(1)); HX|10>=H|11> p.addStep(step2);
SimpleQuantumExecutionEnvironment sqee = new SimpleQuantumExecutionEnvironment(); for (int i=0; i<6; i++){ 6 iterations
Result res = sqee.runProgram(p);
Qubit[] qubits = res.getQubits();
System.out.println(" iteration: " + i);
Arrays.asList(qubits).forEach(q -> System.out.println("qubit with probability on 1 = "+q.getProbability()+", measured it gives "+ q.measure()));
} }
More formally, the above program does exactly the same as the following equation: it brings our initial two-qubits state to the final state H|11> = 1/√2(|01> - |11>)
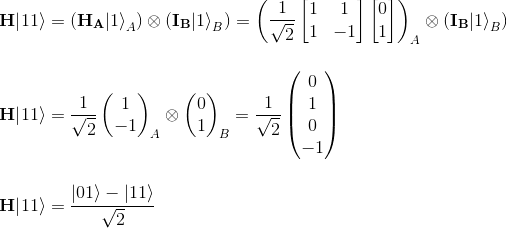
When measured, the first qubit will have 50% (1/√2)2 to be in state |1> and the second qubit will have 100% probability to be observed in state |1>
Fortunately, running our Strange Program confirms this prediction.
Looking at the last line of code
Arrays.asList(qubits).forEach(q -> System.out.println("qubit
with probability on 1 = "+q.getProbability()+", measured it gives "+
q.measure()));
- We iterate on each qubit (via the Java 8 Collection.forEach method),
- Via a java 8 lambda expression, we print the probability for the qubit to be in |1> state by calling the method qubit.getProbability() (thus the probability for the qubit to be in the |0> state would be 1 - this value), as well as the value effectively measured by calling the method q.measure().
When the program is run, on each iteration, we get the probability displayed for each qubit to be in the |1> state. As expected:
- first qubit has 0.49999999999999 = 50% to be in the |1> state
- second qubit has 0.9999999999 = 100% probability to be in the |1> state
Anecdotally, over six runs, we get two times zero as value measured for the first qubit and all the times one as value measured for the second qubit. All good!
Graphical Strange FX API
To visualize all this graphically, Strange API includes a very cool graphic API, Strange FX.
Just add the required import on the beginning of your program, and one line of code at the end
com.gluonhq.strangefx.render.*
Renderer.renderProgram(p);
and you will be able to visualize your quantum circuit and the corresponding output probabilities for each qubit:
C-NOT gate and entanglement
We are just half way to our entanglement state. As we know, we still have to apply the C-NOT gate to the precedent two-qubit state.
With some formula, it translates to:
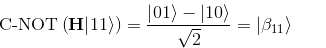
As we remember, the C-NOT gate flips the second qubit of the |10> state to |1> as the first control qubit is |1>.
The corresponding quantum circuit is shown below:
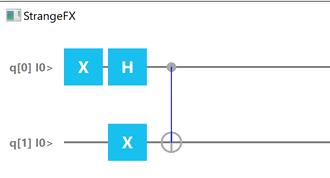
So how can we achieve this via Strange API? Nothing is simpler. We just need to add an another step to our program, which includes the C-NOT gate. This is literally done in two lines
The C-NOT gate takes as parameters the index of our two qubits added initially to our program via the instruction Program p = new Program(2);
Program p = new Program(2); Step step1 = new Step(); step1.addGate(new X(0)); p.addStep(step1); Step step2 = new Step(); step2.addGate(new Hadamard(0)); step2.addGate(new X(1)); p.addStep(step2); Step step3 = new Step(); step3.addGate(new Cnot(0,1)); //we add the Cnote gate here p.addStep(step3);
.....
.....
Renderer.renderProgram(p); //display the probability of each qubit individually Renderer.showProbabilities(p, 1000); //display the 2-qubit final state probabilities over 1000 runs
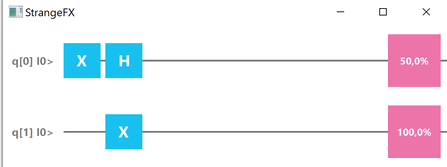
Running this program outputs the following result
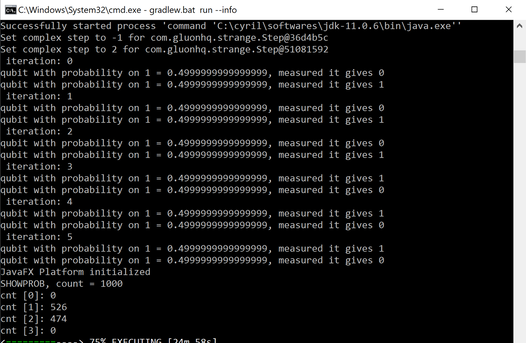
Tha's amazing.
It shows two things:
- each qubit has 50% probability of being observed in the |0> state and so 50% probability of being observed in the |1> state. This is confirmed firstly on our six iterations, as we observe actually three times the first qubit in |0> state and the second qubit in |1> state and the other three times, we observe the opposite, i.e the first qubit in |1> state and the second qubit in |0> state.
This can be vizualized via a single line Renderer.renderProgram(p);

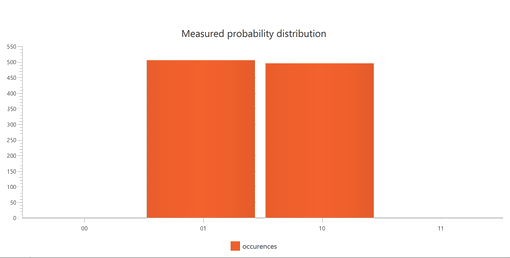
But still this graphic does not show the main interest of this quantum circuit, i.e its entangled nature: we never observe the two-qubit states |00> or |11>.
- To illustrate this fundamental feature, we use the last instruction line Renderer.showProbabilities(p, 1000) which gives the probabilities of the final measured states over 1000 runs: in our case, we measure 526 times |01> and 474 times |10>, but we get a zero probability for both |00> and |11> states.
[1] I have chosen Strange API first because i am a Java developer, and secondly because it offers a nice graphical API.

