|
The gate model of quantum computing consists of:
(1) a set of qubits, sometimes broken up into registers (subsets); (2) an ordered set of quantum gates acting on qubits; (3) a set of measurements on one or more qubits.
This is exactly what we mean by a quantum computer. It’s something that implements operations known as quantum gates on a set of qubits, and then measures some or all of the qubits to get a classical bit as output. The set of operations are ordered in that the order of the gates matters as it determines the algorithm. |
We have so far explained in an easy way the theorical basis of entanglement. How cool it would be to illustrate this abstract articles by a quantum program? Let's first give a quick overview of quantum computing.
Quantum computing has been an increasingly popular research field and source of hype over the last few years. Very recently, Google has even officially announced that it has achieved quantum supremacy in a new article published in the scientific journal Nature. Google says that its 54-qubit Sycamore processor was able to perform a calculation in 200 seconds that would have taken the world’s most powerful supercomputer 10,000 years.
Almost everybody has heard that quantum programs work by asking quantum computing hardware for quantum bits or qubits, quantum analogues of classical bits that we can use to perform some computations. But what is exactly a qubit and how it differs from a classical bit?
Qubits are the basic unit of information in a quantum computer and represent the simplest quantum systems, i.e. the ones described by a two-dimensional Hilbert space. They can be physically implemented by systems that have two states and thus they could be either the quantum coin described in our previous article Introduction to quantum entanglement or more likely the spin electron as exposed in Expectation value of a product state, which is fully described by the combination of the two-basis vectors up and down, or |u> and |d>, or equivalently |1> and |0>.
Say we have classical 3-bit computer: at any moment of time it will be able to store only one of the 23 combinations possibles in memory, by example 101.
On the opposite, a 3-qubit quantum computer will be able to store any combination in the form of:
α|000> + β|001> + γ|010> + δ|011> + ε|100> + ζ|101> + η|110> + θ|111> with:
α, β, γ, δ, ε, ζ, η, θ are eight complex numbers, i.e which can be expressed in the form a + bi, where a and b are real numbers, and i is a solution of the equation x2 = −1 and are called amplitude.
α2 + β2 + γ2 + δ2 + ε2 + ζ2 + η2 + θ2=1[1], i.e the sum of all the probabilities (amplitude squared) equals to one.
By example our 3-qubits system could be in the following state at a given time t
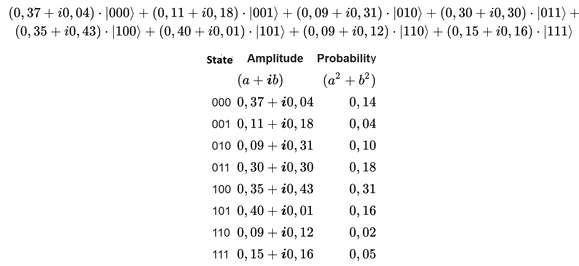
At a given time, the eight complex numbers of the second column are the exact content of the memory of the quantum computer. Of course, it is impossible for us to know anything about these complex numbers during the algorithm processing; that's only at the end that a measure will output a triplet of classical bits, by example 110.
If we had N qubits, we would have 2N lines in the above table. And with around 300 qbits, we would have more lines than the number of atoms in the entire observable universe!
What does it mean is where a classical computer needs 2N operations to do an elementary operation on N classical bits, a quantum computer would need only one quantum operation with N qubits (or rather 2N operations done in parallel). It is important to understand that all these 2N parallel operations are not due to machines or processors working in parallel but rather to the dimension, strictly greater to one, of the space of each q-bit[2],
If we have a classical function calculate taking 3 bits (or boolean as parameters), to process all eight possible triplets, we would need eight distinct operations so that in pseudo-code this could be written as:
for each combination (boolan bit1, boolean bit2, boolean bit3) { // 8 combinations
function calculate (bit1, bit2, bit3)
do some calculation with bit1, bit2 and bit3
return result;
}
}
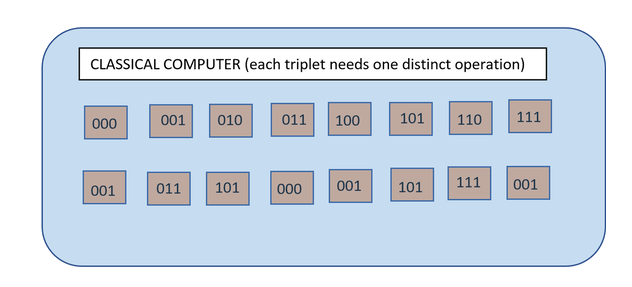
whereas the quantum computer, with one triplet (generally |000>) as input, will process all the possible triplets simultaneously and will output a unique 3-bits combination. Hence one unique quantum processing replaces eight classical operations[3].
In pseudo-code if we have a function calculate taking 3 bits (or boolean as parameters)
function calculate (boolean bit1, boolean bit2, boolean bit3) {
do one operation with all the combinations of bit1, bit2 and bit3 // 1 operation with 3 qubits in superposition state
return result; // one unique triplet
}
}
In the below diagram, each probability to measure at a given time the given triplet (third column a2 + b2 of the precedent table) is represented by a blue rectangle (the sum of all rectangles equals to 1)
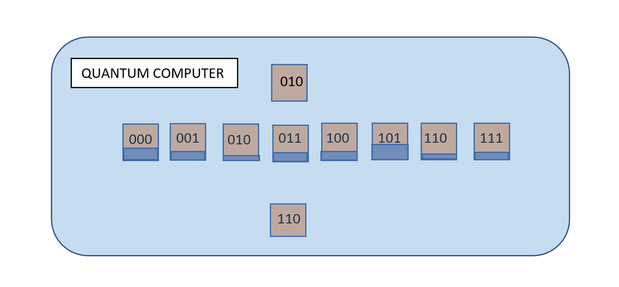
Heuristically, and at the risk of over-simplifying, quantum parallelism allows quantum computers to evaluate a function f(x) for many different values of x simultaneously. We will go through an example of quantum parallelism in our article The Deutsch-Jozsa algorithm.
This being said, we are still learning about the exact extent of what quantum computers are capable of. So far, we have found some examples of problems where quantum computers offer significant advantages over the best known classical approaches. In each case, the quantum algorithms that have been found to solve these problems exploit quantum effects to achieve the advantages, sometimes referred to as a quantum advantage[4].
Some useful quantum algorithms which have been discovered so far:
• The Deutsch-Jozsa algorithm: determines if a function is constant or balanced in one single step.
• Grover’s algorithm: searches a list of N items in √N steps.
• Shor’s algorithm : quickly factors large integers, such as those used by cryptography to protect private data[5].
As a last point, quantum states are quite fragile and sensitive to the external perturbations (like magnetic perturbations for a 1/2 spin) and they don't stick around for very long, which is why quantum computers are currently hard to build.
To summarize:
- All computing systems rely on a fundamental ability to store and manipulate information. Current computers manipulate individual bits, which store information as binary 0 and 1 states. Quantum computers leverage quantum mechanical phenomena to manipulate superposition of two-dimensionnal states. To do this, they rely on quantum bits, or qubits. There are different physical phenomenons that lead to a quantum two-state system - en.wikipedia.org/wiki/Quantum_computing#Developments list those.
- How different q-bits are from their classical counterparts, it is thus very important to keep in mind that measurement outcomes of qubits are classical bit values! Put differently, whether we measure a classical bit or a qubit, our result is always a classical bit. In quantum computing, the exponential power only applies during processing — and not during measurement.
- Comparatively to the N-bits classical computers, N-qbits quantum computers could be, only in certain situations - those where a quantum advantage exists, exponentially more powerful by doing 2N operations in parallel.
- Quantum computers are hard to build due to the fragility of quantum states. One the greatest challenges is controlling or removing quantum decoherence.
[1] This a very general principle of quantum mechanics that extends to all quantum systems: the state of a system is a represented by a unit (normalized) vector in a vector space of states. That's because the squared magnitudes of the components of the state-vector, along particular basis vectors, represent probabilities for various experimental outcomes - cf Born rule, and all probabilities must sum up to 1.
[2]The more and more popular Many-worlds interpretation may lead to some vertiginous conclusion, as the 2N parallel calculations would be done in 2N parallel universes...
[3]We will see in the next article Parallel superposition and Hadamard gates how many quantum algorithms use the Hadamard gate as an initial step, since it maps n qubits initialized with |0> to a superposition of all 2n orthogonal states in the {|0>,|1>}n basis with equal weight.
[4]Finding a provable advantage for a practical problem is an active area of research in quantum computing.
[5]There is a reasonable chance that a number of existing communication protocols and encryption techniques will become vulnerable once quantum computers become more powerful.

