We have already shown how to derive the geodesic equation directly from the Equivalence Principle in in our article Geodesic equation and Christoffel symbols.
Here our aim is to focus on the second definition of the geodesic (path of longer Proper Time[1]) to derive the Geodesic Equation from a variationnal approach, using the Principle of least Action. That's actually how Einstein deduced it in his 1916 synthetic paper The Foundation of the General Relativity of Relativity
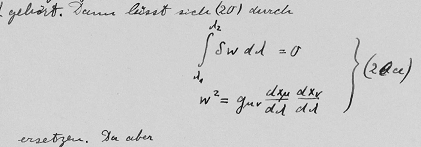
We can express the proper time along a time-like wordline (while ignoring the limits) as:

with λ being the affine parameter parametrizing the path.
For a given proper spacetime interval ds2 = gμνdxμdxν, we get:
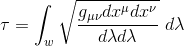
But according to the calculus of variations, finding the path with maximal proper time is equivalent to find the path with extremal action[2] (in this case a maximum), with the action S and the integrated Lagrangian L defined as:
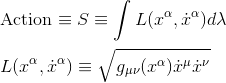
where the dot over the x denotes the derivative with respect to λ.
Passing the above Lagrangian through the Euler-Lagrange equation gives:
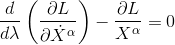
For the four-dimensional space-time, as the indice α can take four values, this equation represent four differential equations.
Looking at the first member and remembering that the metric only depends on xα (and not on the dot/derivatives coordinates), we get using the usual derivative rules

We can now remark that from the above definition of τ, we can write dτ as:
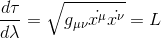
Applying the chain rule we finally obtain
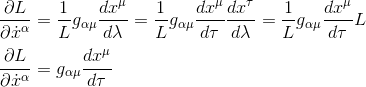
Similarly, considering the second term δL/δxα of the Euler-Lagrange equation:
This section of the article is only available for our subscribers. Please click here to subscribe to a subscription plan to view this part of the article.