If our aim is to find the relativistic generalization of Poisson 's equation for the gravitational field:
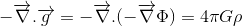
where Φ refers to the gravitational potential and ρ to the mass density, we are half way.
Indeed, we have already seen in our previous article The energy-momentum tensor that the generalisation of the mass density (right hand term of the equation) corresponds to the energy-momentum Tμν.
It seems reasonable then to assume that our equation should take the form of:

where k stands for a scalar and Gμν, called the Einstein tensor represents a rank-2 tensor describing the spacetime curvature .
As far as we know, Gμν should obey the following constraints:
- it should nullify in flat spacetime
- it should describe the spacetime curvature and be linear with respect to Riemann tensor
- it should be symmetric and of rank 2 (as Tμν)
- it should have a null divergence (as Tμν)
- and finally, in Newtonian limits, it should reduce to 4πGρ
First attempt with Ricci tensor as solution
We recall from our article The Geodesic equation in the Newtonian Limit that the gravitational potential Φ is linked to the 00-component of the metric via h00=(g00-1)/c2

It seems then natural to look for a tensor which involves the second derivatives of the metric, which is the case for the Riemann tensor. Furthemore, the Riemann tensor is the only candidate that we know so far to being able to describe the spacetime curvature (cf second constraint above).
As we have to find a rank-2 tensor, and if we assume that we have to find a solution solely in terms of the Riemann tensor, it seem natural to first consider the contracted form of the Riemann tensor, known as the Ricci tensor[1].
To see this, let us recall the expression of the Riemann tensor from tha article The Riemann curvature tensor part II: derivation from the geodesic deviation
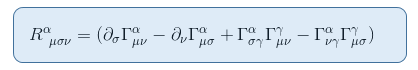
In the limit of a static and weak gravitational field, only one term contributes to R00:
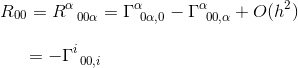
In the same article, we have calculated this Christoffel symbol and found that

with the approximation of gij = ηij and goo,j = hoo,j (refer to the article) we get:
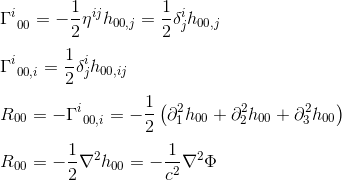
The identification of R00 with ΔΦ (Laplacian operator) suggests that the field equation in general relativity should equate Rab to a constant multiple of Tab.
In 1915, using this equation, Einstein was even able to resolve the long standing problem of Mercury perihelion precession, causing to write in November of that year that, "For a few days, i was beside myself wih joyous excitement."
Eventually, Einstein had to reject this first attempt, due to the fact that in general divergence of Rab does NOT nullify.
Second attempt
There is tensor closely related to the Ricci scalar wihch can be put on the left-hand side without contradiction. This gives the Einstein tensor defined as follows:

where R = Raa is the Ricci scalar or scalar curvature.
This form of Gab is symmetrical and of rank-2 and obviously describes the spacetime curvature. So it just remains to show that the total derivative is zero
To do this, we start with the The Bianchi identity
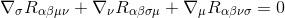
Multiplying through by gγσgαμgβν (the metrics derivatives are zero, so they act as constants and can be taken inside the derivatives), it yields to:
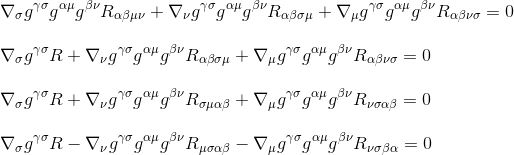
By using the Ricci tensor definition Rμν=gμβgνσRβσ (step 3) and by renaming the indices (step 4), we get
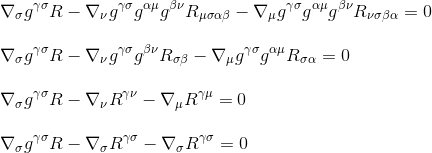
By factorising the derivative, we finally obtain
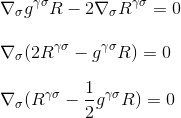
which is exactly what we wanted to demonstrate: the divergence of Einstein tensor is null, and we have found the right candidate for the left hand side of our curvature/mass-energy equation.
[1] Einstein and Grossmann have had already suggested the Ricci tensor as a potential candidate for the gravitationnal tensor in 1913, but did reject it for wrong reasons. Refer to the article 1913 The Entwurf or the missed occasion for more details

