Riemann curvature tensor and Ricci tensor for the 2-d surface of a sphere

Our aim is to get more familiar with the Riemann curvature tensor and to calculate its components for a two-dimensional surface of a sphere of radius r.

First let's remark that for a two-dimensional space such as the surface of a sphere, the Riemann curvature tensor has only one not null independent component.

Actually as we know from our previous article The Riemann curvature tensor part III: Symmetries and independant components, the first pair and last pair of indices must both consist of different values in order for the component to be (possibly) non-zero. Therefore, in two dimensional space where each indice could only take the values 0 and 1, the only possibility for each pair is to contain these distinct indices 0 and 1, which represent the coordinates θ and φ in polar coordinates.

So, over 2^4 = 16 components of the Riemann tensor in two-dimensional space, only one component is independent and not null.

If we choose this component to be R_θφθφ for example, then we can easily deduce the three other not null components by using the Riemann tensor symmetries:

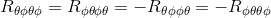
Therefore, we only have to calculate the first term R_θφθφ

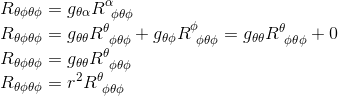
Indeed, we recall from our article The Riemann curvature tensor for the surface of a sphere that the spacetime interval on the surface of a sphere of radius r in polar coordinates is:

ds² = r²dθ² + r²sin²θdΦ²

So that we get as the corresponding metric g_ij:

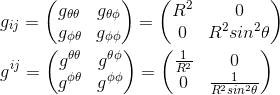
 which means that g_θφ=0 and that g_θθ=r²

As the expression of the Riemann tensor as deduced in The Riemann curvature tensor part II: derivation from the geodesic deviation is given by

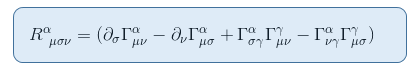
If we substitute the indices for R^θ_φθφ ,the above equation becomes