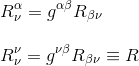As we will see later, the Bianchi Identity equation will be of fundamental importance to find the Einstein equation.
Also the complete, unalterated form of the Riemann curvature tensor doesn't appear in the Einstein field equations. Instead, it is contracted to give two other important measures of the curvature known as the Ricci tensor and the Ricci scalar.
In this article, our aim is to define these three important Rieman tensor derivatives.
The Bianchi Identity
First let us try to demonstrate the Bianchi Identity

From our previous article The Riemann curvature tensor part III: Symmetries and independant components, we know that at the origin of a Local Inertial Frame (LIF), we have:
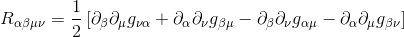
We also know from Introduction to Covariant Differentiation that at the origin of Local Inertial Frame, the Christoffel symbols do all vanish, and then the covariant derivative becomes the ordinary derivative:

Therefore, we get, at the origin of a LIF:
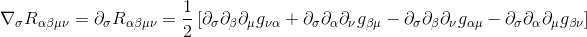
By cyclically permuting the index of the derivative with the last two indices of the tensor, we get:
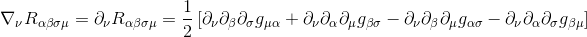
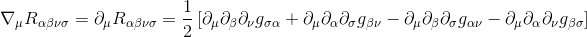
By adding up these the three equations and using the commutativity of partial derivatives, we see that the terms cancel in pairs, so we get what we want
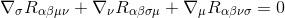
The Ricci tensor and Ricci scalar
First, we can contract the first and third indices of the Riemann curvature tensor to get the Ricci tensor
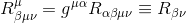
Using both the Riemann tensor and metric symmetries, we show easily that the Ricci tensor itself is symmetric
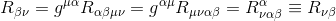
so the Ricci tensor is symmetric.
We can contract the Ricci tensor in turn to get the curvature scalar or Ricci scalar R