In our two previous articles, we have deduced the rather complicated expression of the Riemann curvature tensor, a glorious mixture of derivatives and products of connection coefficients, with 256 (=4^4) components in four-dimensional spacetime.
But we have also demonstrated in our article Local Flatness or Local Inertial Frames and SpaceTime curvature that any arbitrary coordinate system could nullify all but 20 second derivatives of a given metric in a curved spacetime. Our aim in this article is to demonstrate that the Riemann tensor has only 20 independant components and that these component are precisely a combination of these second not null derivatives.
The methodology to adopt there is to study the Riemann tensor symmetries in a Local Inertial Frame (LIF) - where as we know all the Christoffel symbols are null - and to generalize these symmetries to any reference frame, as by definition a tensor equation valid in a given referential will hold true in any other referential frame.
Using the definition of the Riemann tensor as seen in the precedent articles:
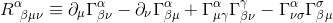
and knowing that all the Christoffel symbols are null at the origin of Local Inertial Frame, this expression get simplified to:
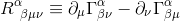
By applying the contraction mechanism as exposed in Introduction to Tensors, we can rewrite the Riemann tensor with all indices lowered:
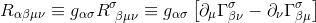
We remember from our article Christoffel symbols in terms of the metric tensor how to write the Christoffel symbol with respect to the metric derivatives:
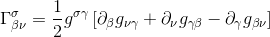
So that we can write
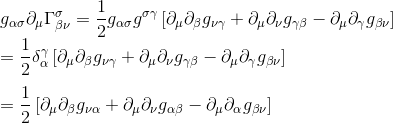
By substituting indices μ and ν, we get the second term of the Riemann tensor expression:
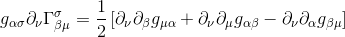
By substracting the two expressions we see that the middle terms cancel, so we’re left with:
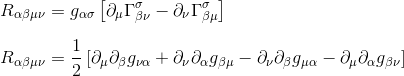
This could obviously be written as:
This section of the article is only available for our subscribers. Please click here to subscribe to a subscription plan to view this part of the article.

