In our previous article Local Flatness or Local Inertial Frames and SpaceTime curvature, we have come to the conclusion that in a curved spacetime, it was impossible to find a frame for which all of the second derivatives of the metric tensor could be null.
We have also mentionned the name of the most important tensor in General Relativity, i.e. the tensor in which all this curvature information is embedded: the Riemann tensor - named after the nineteenth-century German mathematician Bernhard Riemann - or curvature tensor. In other words, the vanishing of the Riemann tensor is both a necessary and sufficient condition for Euclidean - flat - space.
In this article, our aim is to try to derive its exact expression from the concept of parallel transport of vectors/tensors.

Parallel transport
Say you start at the north pole holding a javelin that points horizontally in some direction, and you carry the javelin to the equator, always keeping the javelin pointing "in as same a direction as possible", subject to the constraint that it point horizontally, i.e., tangent to the earth. (The idea is that we're taking "space" to be the 2-dimensional surface of the earth, and the javelin is the "little arrow" or "tangent vector", which must remain tangent to "space".)
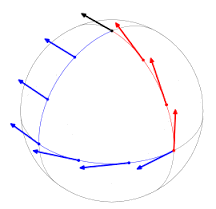
After marching down to the equator, march 90 degrees around the equator, and then march back up to the north pole, always keeping the javelin pointing horizontally and "in as same a direction as possible" along the meridian.
By the time you get back to the north pole, the javelin is pointing a different direction! That's because the surface of the earth is curved. In fact, if we parallel transport a vector around an infinitesimal loop on a manifold, the vector we end up wih will only be equal to the vector we started with if the manifold is flat.
Actually, "parallel transport" has a very precise definition in curved space: it is defined as transport for which the covariant derivative - as defined previously in Introduction to Covariant Differentiation - is zero.
So holding the covariant at zero while transporting a vector around a small loop is one way to derive the Riemann tensor.
But there is also another more indirect way using what is called the commutator of the covariant derivative of a vector.
Covariant derivative commutator
In this usage, "commutator" refers to the difference that results from performing two operations first in one order and then in the reverse order. So if one operator is denoted by A and another is denoted by B, the commutator is defined as [AB] = AB - BA. Thus if the sequence of the two operations has no impact on the result, the commutator has a value of zero.
To get the Riemann tensor, the operation of choice is covariant derivative. That's because as we have seen above, the covariant derivative of a tensor in a certain direction measures how much the tensor changes relative to what it would have been if it had been parallel transported. The commutator of two covariant derivatives, then, measures the difference between parallel transporting the tensor first one way and then the other, versus the opposite.
In flat space the order of covariant differentiation makes no difference - as covariant differentiation reduces to partial differentiation -, so the commutator must yield zero. Inversely, any non-zero result of applying the commutator to covariant differentiation can therefore be attributed to the curvature of the space, and therefore to the Riemann tensor.
Derivation of the Riemann tensor
So, our aim is to derive the Riemann tensor by finding the commutator
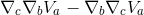
or, in semi-colon notation,
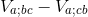
We know that the covariant derivative of Va is given by

Also, taking the covariant derivative of this expression, which is a tensor of rank 2 we get:
This section of the article is only available for our subscribers. Please click here to subscribe to a subscription plan to view this part of the article.
We define the expression inside the brackets on the right-hand side to be the Riemann tensor, meaning
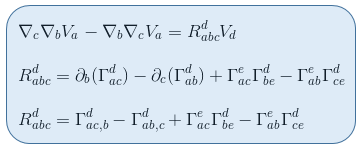
Remark 1: The curvature tensor measures noncommutativity of the covariant derivative as those commute only if the Riemann tensor is null.
Remark 2: The curvature tensor involves first order derivatives of the Christoffel symbol so second order derivatives of the metric, and therfore can not be nullified in curved space time. We recalll from our article Local Flatness or Local Inertial Frames and SpaceTime curvature that if the surface is curved, we can not find a frame for which all of the second derivatives of the metric could be null.
Remark 3: Having four indices, in n-dimensions the Riemann curvature tensor has n4 components, i.e 24 = 16 in two-dimensional space, 34=81 in three dimensions and 44=256 in four dimensions (as in spacetime).

