After spending some time looking at tensors, we can now expose the problem of how to differentiate a tensor in curved spacetime.
To work with tensor components, one would need a set of basis vectors {eα} as well as the dual set of basis 1-forms (wα). In flat spacetime a single such basis suffices; all events can use the same Lorentz basis. But not in curved spacetime!
There each event has its own tangent space, and each tangent space requires a basis of its own.
To compare two vector and tensors at neighboring events along a curve, one has to parallel transport their basis, compare them, and sees the bases twist and turn. They must do so, in order to to accomodate themselves to the curvature of spacetime.
To quantify the twisting and turning of basis vectors and forms, one has to use the covariant derivative.
Examine the changes in vector fields along a basis vector eβ is noted:
∇eβ which is also noted as ∇β
And especially examine the rate of change of some basis vector eα is noted ∇βeα
Covariant differentiation for a contravariant vector
Consider a vector V = Vαeα (ie the tensor has contravariant components Vα and coordinate basis vectors eα). Using the product rule of derivation, the rate of change of the components Vα (of the vector V) with respect to xβ.
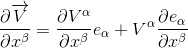
But we recall from our article Christoffel Symbol or Connection coefficient that the connection coefficients are defined by:
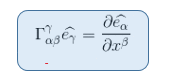
Substituing this expression in the above equation gives

The right hand term has two dummy indices (ie indices to be summed over) α and γ. We can improve the formula by changing α to γ and γ to α to give:
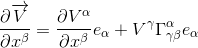
and factoring out eα gives
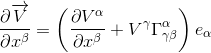
This expression indicates the rate of change of Vα in each of the directions β of the coordinate system xβ, and is known as the covariant derivative of the contravariant vector V. The nabla symbol is used to denote the covariant derivative
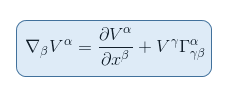
In words: the covariant derivative is the usual derivative along the coordinates with correction terms which tell how the coordinates change.
The intesting property about the covariant derivative is that, as opposed to the usual directional derivative, this quantity transforms like a tensor, i.e. it is independant of the manner in which it is expressed in a coordinate system.
Remark 1: As we have seen in our articles Local Flatness or Local Inertial Frames and SpaceTime curvature and Local Inertial Frame (LIF), in a inertial frame of reference, the vanishing of the partial derivatives of the metric tensor at any point of M is equivalent to the vanishing of Christoffel symbols, and then we can write this fundamental equality in the context of any inertial or local inertial frame:

Remark 2:
This section of the article is only available for our subscribers. Please click here to subscribe to a subscription plan to view this part of the article.

