Einstein Relatively Easy

Tweet

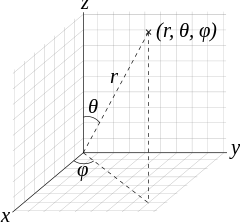
In this article, we will calculate the Euclidian metric tensor for a surface of a sphere in spherical coordinates by two ways, as seen in the previous article Generalisation of the metric tensor

• - By deducing the metric directly from the space line element
• - By calculating the metric from the product of derivatives of the two-dimensional Cartesian coordinates system

Deducing the metric by the line element

In this Euclidian three-dimensionnal space, the line element is given by:

dl² = dr² + r²dθ² + r²sin²θdΦ²

If we set the polar coordinate r to be some constant R we lose the dr term (because r is now constant) and the line element now becomes: 

dl² = R²dθ² + R²sin²θdΦ²

which describes a two-dimensional surface using the two polar coordinates (θ, Φ)

Or we know from the previous article that this line element could be written as:

dl² = g_ijdxⁱdy^j

We can deduce immediately that the metric and inverse metric for this surface, using coordinates x⁰=θ and x¹=Φ, are:

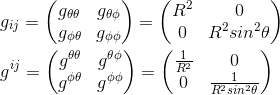
This was the easy part. Let's try to calculate the same metric by using  the formula of the coordinates derivatives product.

Calculating the metric by the Cartesian  coordinates derivatives product

We should recall that we also defined the metric tensor as the product of derivatives to another coordinate system (in the previous article, it was from a Minkowski inertial referential)

 Or the cartesian coordinates and spherical coordinates are linked together by the following equations:

At this point we can confirm that by both the space  line element and the product of coordinates derivatives, we have found exactly the same components for the metric of a two-dimensional surface of a sphere in polar coordinates