In 1911 the The Equivalence Principle led Einstein to believe that light would be deflected in the presence of a gravitational field.
It wasn't until 1915, however, after he had successfully incorporated curved spacetime into a gravitational theory of relativity, that he was able to make an accurate prediction as to the magnitude of such a deflection.
Returning to the mathematics, we have seen in our previous article Geodesics in Schwarzschild spacetime that the Schwarzschild geodesic equations can be used to derive null geodesic equations that describe the path of a light ray in spacetime.
Ultimately, for this purpose, we would like to express r as a function of Φ
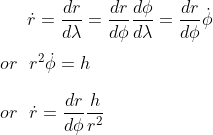
Let's define u = 1/r
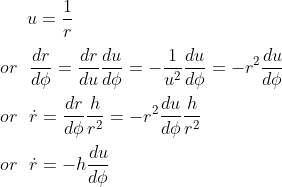
Replacing this expression in our original geodesic equation leads to
This section of the article is only available for our subscribers. Please click here to subscribe to a subscription plan to view this part of the article.
The deflection is symetric with respect to Φ = π/2, and replacing the light speed by its real value c (in the Schwarzschild expression above we assumed c=1), gives
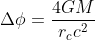
Example of the light deflection near the Sun
Let's calculate the deflection near the Sun, taking the following values:
G = 6.67 x 10-11 SI
M = 2 x 1030 kg
R0 = 700 000 km
c = 3 x 108 ms-1
gives ΔΦ = 8.5 x 10-6 rad = 4.85 x 10-4 degrees = 0.029 ' = 1.74''
That's the value that Eddington confirmed in his famous Eddington experiment during total solar eclipse of 29 May 1919.