Schwarzschild metric derivation

               After a quick introduction to the Schwarzschild metric solution, it is now time to derive it.

According to his letter from 22 december 1915, Schwarzschild started out from the approximate solution in Einstein’s “perihelion paper”, published November 25th.

We will go through a more formal derivation, which could be broken down into the following steps:

- simplify the metric for  a static and spherically symmetric solution with some coefficients as functions f(r), i.e depending on r only.

- deduce the corresponding Christoffel symbols

- calculate the Ricci tensor components

- deduce the exact form of the above coefficient functions f(r)  by setting the above Ricci tensor components as null as they should be in vacuum.

Step 1 - Expression of the metric tensor for a static and spherically symmetric solution

We recall that in space-time the distance interval has the following form

In spherical coordinates t, r, θ, φ (which makes sense in case of a spherical solution..), the spacetime interval can be expanded as below:

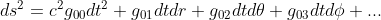
First of all, because the solution is static, it should not depend on time. In particular, a change from t -> -t  should not change anything (time reversible), So that we should not have any croseed term in the form of dtdr, dtdθ or dtdφ, but only of the form dt².

Then, taking in account the spherical symmetry, we can start out by the Minkowski metric written in spherical coordinates:

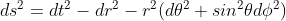
We are free to multiply the terms by any arbitrary r-dependent coefficients, leading to:

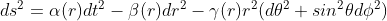
where α(r), β(r) and γ(r) represent some unkwnown functions of r.

In this metric, the coordinate r is the usual radial distance from the origin (the center of the source mass). I we assume that γ(r)=1, we have changed r and can no longer assume that it is the simple radial distance from the origin. This step makes sense, however, as we can rewrite the metric as simply:

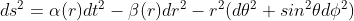
We have just absorbed γ(r) by a redefnition of r (replace r by example by r'=√γ(r)r)

We note that this proposed metric has the following properties:

- none of the metric components depend on time - meaning the metric is static.

- if we let r and t be constant, then dt² = 0 and dr² = 0 and the metric becomes

      ds² = r²(dθ² + sin²θdφ²)

which is the line element for the surface of a sphere - meaning the metric is spherically symmetric.

- the functions α(r) and  β(r) must be consistent with T_μν = 0 (empty spacetime in the vicinity of a source mass)

- both α(r) and  β(r) must approach 1 as r approaches infinity, to become the Minkowski metric in spherical coordinates (the metric should be asymptotic flat)

Step 2 - Finding the connection coefficients

We recall the expression of the connection coefficient relative to the metric components g_μν:

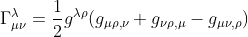
as well as the meaning of the superscript and subscript variables of the connection coefficient (refer to the article Christoffel Symbol or Connection coefficient for more details)

In the below image, the subscript index α specifies the basis vector for which the derivative is being taken, the index β denotes the coordinates being varied to induce this change in the αth basis vector, and the index γ identifies the direction in which this component of the derivatives points:

Thus the below equation should be read as follows in two-dimensionna space: the change in e_r caused by a change in θ has zero magnitude in the e_r direction, and the change in e_r caused by a change in θ varies inversely with distance in the e_θ direction.

 We have to find the four following different coefficients:

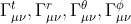
with μ and ν taking themselves the four values t, r, Θ and φ hence a total of 4 x 16 = 64 values.

But actually, as we recall from the Christoffel symbol definition, by symmetry of the lower indices, we just have 10 independant values for each coefficient, so that the 64 values reduce to only 40 independant values (10 for each Christoffel symbol).

Let's start with the expression of Γ^t_μν:

Writing the proposed metric in its matrix form for more lisibility

so that our proposed metric takes the following form

From our previous article Geodesic equation in the Newtonian Limit, we know that at the Newtonian limit

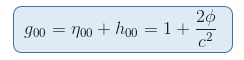
so that

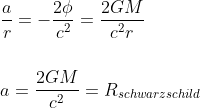
and will retieve the final form of the Schwarzschild metric as introduced in our previous article

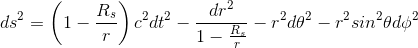
If we magic away our star so that M=0, then R_s=0 and the Schwarzschild metric reverts again to the flat Minkowski metric of special relativity expressed in spherical coordinates.

Only when M=0 do the coordinates t and r represent real clock-time and radial distance from the center of the mass. If we increase M we start to curve spacetime and we can no longer assume that t and r correspond to these measurable quantities.

Step 6 - Calculating the Earth and the Sun Schwarzschild radius

Assuming that they are both spherically symmetric bodies, we can  calculate the Schwarzschild radius of the Earth and the Sun.

Starting with the Earth, using the mass of the Earth = 5.97 x 10²⁴ kg, and the gravitational constant G = 6.67 x 10^-11 Nm²kg^-2  we have:

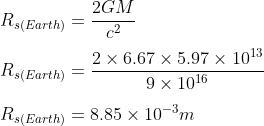
or about 9 millimeters. The actual radius of the Earth is about 6370km.

Given the mass of the Sun  = 1.99 x 10³⁰ kg, the same calculus gives

or about 3km. The actual radius of the Sun is about 696,000 km.

The most noticeable property of the Schwarzschild radius is that if all of the mass M could be squeezed inside of sphere of radius R_s, light would not be able to escape from the object and we would have created a black hole.

From the previous calculus we can see that if we wanted to transform the Earth into a black hole, we would need to squash it down into a  9mm radius sphere.