After having derived the Einstein equation by the historical way (refer to Einstein Field Equations) and through the more modern lagragian road (see Einstein-Hilbert action), it is now time to seek for a solution.
Minkowski spacetime is usually known as a 'trivial' solution to the Einstein field equations. Triviality meaning that both the energy momentum tensor and the Riemann curvature tensor equal to zero.
Trying to give an exact solution to the Einstein equations which do not reduce to Minkowski flat spacetime is notorious difficult. Einstein himself used approximation methods when working out the predictions of general relativity [1] - in the same way it is common to use approximation when looking at the Newtonian limit (weak, static gravitational fields and slow moving particles) by assuming the metric to be gμν = ημν + hμν, refer by example to our previous article Geodesic equation in the Newtonian Limit.
That's why Einstein was so pleasantly surprised when in 1916, shortly after he had proposed his general theory of relativity, a German astrophysicist Karl Schwarzschild published an exact solution to the field equations. That's how Einstein's letter from 16 January 1916 to Schwarzschild [2] begin:
"Highly esteemed Colleague, I examined your paper with great interest. I would not have expected that the exact solution to the problem could be formulated so simply. The mathematical treatment of the subject appeals to me exceedingly. Next Thursday I am going to deliver the paper before the Academy with a few words of explanation."
The Schwarzschild metric describes a static, spherically symmetric gravitationnal field in the empty region of spactime near a massive spherical object. Strictly speaking, the solution only applies to non-rotating spherical masses. However, the Schwarzschild metric also provides a good approximation to the gravitationnal field of slowly rotating bodies such as the Sun or Earth.
In that sense, the Schwarzschild solution can be viewed as the first and arguably the most important non-trivial solution of the Einstein field equations.
In this article, we will simply state the Schwarzschild metric just to get a glimpse of its form, so at least we know what it looks like. We will go through the derivation in the next articles.
Here is the full version:
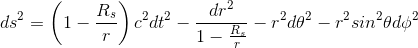
The quantity Rs is known as the Schwarzschild radius as:
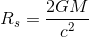
[1] In his famous paper D.24 Explanation of the perihelion Motion of Mercury from the General Theory of Relativity, Einstein uses explicitly two approximations, that we will detail in a future article.
"I assume in what follows that the guv differ from the values given in equation (4a) only by quantities small compared to unity. "
[2] Letter from Albert Einstein to Karl Schwarzschild from 9th January 1916.

