Dans cet article, notre intention est de dériver l'expression d'une géodésique depuis sa déifnition de ligne d'univers de temps propre maximal.
Considérons deux événements A et B séparés par un intervalle de genre temps, et paramétrons la trajectoire qui les lie par un paramètre λ qui va de 0 en A à 1 en B, c'est-à-dire en spécifiant xμ(λ).
Le temps propre mesuré le long de la ligne d'univers s'écrit alors:
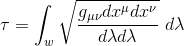
Trouver la ligne d'univers de plus long temps propre revient à trouver la trajectoire (xα) dictée par le principe variationnel de la mécanique.
Dans ce cadre, on exprime l'action S du système comme l'intégrale sur le paramètre λ du lagrangien L défini ci-dessous:
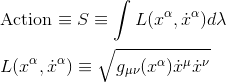
avec x.μ représentant la "vitesse" par rapport au paramètre λ.
La ligne d'univers que l'on recherche est celle qui satisfait l'équation d'Euler-Lagrange pour ce lagrangien
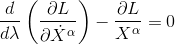
Dans le cadre de l'espace-temps quadri-dimensionnelle, cela représente quatre équations différentielles, une pour chaque valeur de l'indice abstrait α.
En développant la dérivée et en se souvenant que la métrique ne dépend pas de la dérivée de xα mais simplement de xα,

On peut à présent remarquer que d'après la définition du temps propre tau vue plus haut on peut exprimer sa dérivée sous la forme:
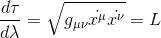
En reportant cette identité dans l'équation précédente et en appliquant la règle de dérivation en chaîne
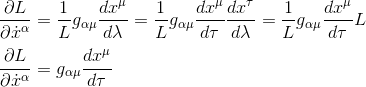
De même si l'on considère le terme δL/δxα de l'équation d'Euler-Lagrange:
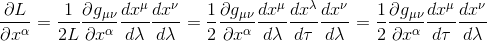
et l'équation d'Euler-Lagrange devient donc, en renommant l'indice μ en β dans le premier terme de l'équation car la première somme implicite est indépendante de celle du second membre
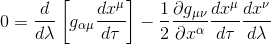
Finalement, en mulitpliant les deux membres de l'équation par dλ/dτ donne:
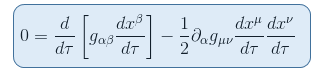
Il s'agit de l'équation des géodésiques sous la fome où on l'utilise le plus souvent.
Remarque: le résultat précédent ne peut plus étre considéré comme valide dans le cas des photons, car le temps propre mesuré le long de la ligne d'univers suivie par la lumière est toujours nul.